500г олова нагрели и расплавили.Определите количество теплоты затраченное при этом, если начальная темп. олова была 12°С (с=250Дж/кг°С;темп.плавления олова 232°С; лямбда олова 5,9×10(6)Дж/кг)
Найти потенциал шара радиуса R = 0,1 м, если на расстоянии r=10м от его поверхности потенциал электрического поля 
Поле вне шара совпадает с полем точечного заряда, равною заряду q шара и помещенного в его центре. Поэтому потенциал в точке, находящейся на расстоянии R + r от центра шара, jr= kq/(R + r); отсюда q = (R + r)jr/k. Потенциал на поверхности шара

2 N одинаковых шарообразных капелек ртути одноименно заряжены до одного и того же потенциала j. Каков будет потенциал Ф большой капли ртути, получившейся в результате слияния этих капель?
Пусть заряд и радиус каждой капельки ртути равны q и r. Тогда ее потенциал j = kq/r. Заряд большой капли Q = Nq, и если ее радиус равен R, то ее потенциал Ф = kQ/R = kNq/R = Njr/R. Объемы маленькой и большой капель  и  связаны между собой соотношением V=Nu. Следовательно,  и потенциал

3 В центре металлической сферы радиуса R = 1 м, несущей положительный заряд Q=10нКл, находится маленький шарик с положительным или отрицательным зарядом |q| = 20 нКл. Найти потенциал j электрического поля в точке, находящейся на расстоянии r=10R от центра сферы.
В результате электростатической индукции на внешней и внутренней поверхностях сферы появятся равные по модулю, но противоположные по знаку заряды (см. задачу 25 и рис. 332). Вне сферы потенциалы электрических полей, создаваемых этими зарядами, в любой точке равны по модулю и противоположны по знаку. Поэтому потенциал суммарного поля индуцированных зарядов равен нулю. Таким образом, остаются лишь поля, создаваемые вне сферы зарядом BQ на ее поверхности и зарядом шарика q. Потенциал первого поля в точке удаленной от центра сферы на расстояние r, , а потенциал второго поля в той же точке . Полный потенциал . При q=+20нКл j=27В; при q=-20нКл j=-9В.
Формула сопротивления последовательного соединения и параллельного.
С формулы параллельного соединения мы сможем определить сопротивления на соответствующих участках, а с формула последовательного - получить общее сопротивление.
1)Элемент с тремя параллельными.
Т.к все резисторы имеют одинаковое сопротивление то можно записать так.
Из этого следует, что
2)Элемент с 3 параллельными, два из которых двухэлементные.
Тут всё по такому же принципу, но в участках где 2 резистора в ряду, из общее сопротивление будет 20.
Ну а так как 2 и 3 ряды одинаковые то их сопротивление можно обозначить одной буквой.
Подведём к общему знаменателю и сложим дроби.
3)Теперь у нас есть сопротивление на всех участках цепи.
Осталось сложить по формуле последовательного соединения все элементы.
Найти потенциал шара радиуса R = 0,1 м, если на расстоянии r=10м от его поверхности потенциал электрического поля 
Поле вне шара совпадает с полем точечного заряда, равною заряду q шара и помещенного в его центре. Поэтому потенциал в точке, находящейся на расстоянии R + r от центра шара, jr= kq/(R + r); отсюда q = (R + r)jr/k. Потенциал на поверхности шара

2 N одинаковых шарообразных капелек ртути одноименно заряжены до одного и того же потенциала j. Каков будет потенциал Ф большой капли ртути, получившейся в результате слияния этих капель?
Пусть заряд и радиус каждой капельки ртути равны q и r. Тогда ее потенциал j = kq/r. Заряд большой капли Q = Nq, и если ее радиус равен R, то ее потенциал Ф = kQ/R = kNq/R = Njr/R. Объемы маленькой и большой капель  и  связаны между собой соотношением V=Nu. Следовательно,  и потенциал

3 В центре металлической сферы радиуса R = 1 м, несущей положительный заряд Q=10нКл, находится маленький шарик с положительным или отрицательным зарядом |q| = 20 нКл. Найти потенциал j электрического поля в точке, находящейся на расстоянии r=10R от центра сферы.
В результате электростатической индукции на внешней и внутренней поверхностях сферы появятся равные по модулю, но противоположные по знаку заряды (см. задачу 25 и рис. 332). Вне сферы потенциалы электрических полей, создаваемых этими зарядами, в любой точке равны по модулю и противоположны по знаку. Поэтому потенциал суммарного поля индуцированных зарядов равен нулю. Таким образом, остаются лишь поля, создаваемые вне сферы зарядом BQ на ее поверхности и зарядом шарика q. Потенциал первого поля в точке удаленной от центра сферы на расстояние r, , а потенциал второго поля в той же точке . Полный потенциал . При q=+20нКл j=27В; при q=-20нКл j=-9В.
Тут понадобятся две формулы.
Формула сопротивления последовательного соединения и параллельного.
С формулы параллельного соединения мы сможем определить сопротивления на соответствующих участках, а с формула последовательного - получить общее сопротивление.
1)Элемент с тремя параллельными.
Т.к все резисторы имеют одинаковое сопротивление то можно записать так.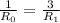
Из этого следует, что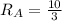
2)Элемент с 3 параллельными, два из которых двухэлементные.
Тут всё по такому же принципу, но в участках где 2 резистора в ряду, из общее сопротивление будет 20.
Ну а так как 2 и 3 ряды одинаковые то их сопротивление можно обозначить одной буквой.
Подведём к общему знаменателю и сложим дроби.
3)Теперь у нас есть сопротивление на всех участках цепи.
Осталось сложить по формуле последовательного соединения все элементы.
И в итоге получаем:
ответ: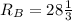 Ом
Ом