Автомобиль проехал половину пути со скоростью 60 км/ч, половину оставшегося времени со скоростью 15 км/ а последний участок — со скорость 45 км/ч. Какова средняя скорость автомобиля на всем пути? (Если что нужно решить две задачи с фото, полностью оформленной задачей)

1502 м

Объяснение:

Поскольку сопротивлением воздуха можно пренебречь, на тело действует только сила тяжести.

Рассмотрим вертикальный и горизонтальный полет отдельно.

Вертикальное движение мяча является равноускоренным с ускорением g.

Горизонтальное движение является равномерным.

Начальная вертикальная скорость:

Начальная горизонтальная скорость:

Полет заканчивается, когда мяч падает на землю.

Найдем время полета:

Получаем обычное квадратное уравнение. Решая его, при условии что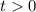 получаем

За это время горизонтально мяч пролетит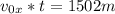

• условимся обозначать индексом 1 автомобиль, а индексом 2 - прицеп

• дабы облегчить дальнейшие расчеты, сразу вычислим значение косинуса угла наклона плоскости к горизонтали:

○ cosα = √(1-0.1²) ≈ 0.994

• напишем уравнения динамики в проекции на ось, направленную вдоль плоскости и сонаправленную с ускорением автомобиля и прицепа (к слову, они равны, так как допускаем, что трос нерастяжимый; силы натяжения равны по 3 закону Ньютона)

○ Fтр - T - m1gsinα = m1a
○ T - m2gsinα = m2a

• сила трения равна по закону Кулона-Амонтона Fтр = u N = u m1gcosα. учитывая это, складываем уравнения:

○ m1g (u cosα - sinα) - m2gsinα = a (m1 + m2)

○ a = (g (m1 (u cosα - sinα) - m2sinα))/(m1 + m2)

• чтобы не допустить в дальнейшем вычислительной ошибки, посчитаем ускорение отдельно:

○ a ≈ 0.6 м/c²

• из уравнения динамики для прицепа получаем:

○ T = m2 (g sinα + a) = 1600 H