Как и было упомянуто раннее, инерция – это своеобразное явление, которое демонстрирует сохранение скорости тела в момент, когда тело НЕ подвержено воздействию других объектов.
Первое утверждение – одно из простейших примеров в теме инерции. Водитель нажимает на тормоз, но при этом машина (тело) имеет определенную массу и вес, а помимо этого во время торможения имеет еще и скорость. Поэтому, на момент когда водитель затормозил – остановка тела происходит не мгновенно, а своевременно, проехав еще несколько метров. Отношение скорости и массы как раз таки образуют то, что названо "инерцией" в этих примерах.
Второе утверждение – аналогично само по себе простое и легко объясняется. Человек аналогично имеет вес и массу, а во время бега еще и скорость, отсюда мы и получаем, что человек бежит → начинает останавливаться ногами, но при этом, положение тела во время бега (туловище наклонено вперед) делает все само за себя.
Поскольку центр масс во время бега смещен, человек не может мгновенно остановится, а лишь постепенно сбавляет скорость и переходит с бега на шаг. Иначе говоря, тормозить начинают лишь ноги, в то время как туловище все еще находится в движении.
Общее между примерами то, что оба тела подвержены скорости, массе и весу, а поэтому, во время движения и остановки – и на машину, и на человека будет действовать инерция.
1)Нам известно, что 1 мм рт. ст. - это 1 метр на земле, надо сделать следующим образом.. . зайти на здание, посмотреть давление, оно должно быть меньше 760 мм рт. ст. , надо от 760 отнять то число, которое получится на высоте здания - это и есть высота здания в метрах!
или
Известно, что при подъеме на высоту 12 метров, давление падает на 1 мм рт ст. Замечаешь давление на земле, поднимаешься на крышу, если давление уменьшилось на 2 мм рт ст, значит высота дома 24 метра. Всё просто.
2)Для этого нужен не только барометр, но и секундомер. Сбросив барометр с крыши здания, секундомером засеките время его падения. Согласно уравнению, описывающему ускоренное движение, путь, пройденный телом в свободном падении, равен , где g — ускорение свободного падения (9,8 м/с^2), а t — время падения. Вычислив по этой формуле дистанцию, которую пролетел барометр до падения на землю, вы получите высоту здания.
3) Мой любимый - Привяжите барометр к длинной веревке и постепенно спускайте его с крыши здания на землю. Как только барометр коснется земли, измерение завершено. Остается только спуститься на землю и любым измерить длину веревки.
Как и было упомянуто раннее, инерция – это своеобразное явление, которое демонстрирует сохранение скорости тела в момент, когда тело НЕ подвержено воздействию других объектов.
Первое утверждение – одно из простейших примеров в теме инерции. Водитель нажимает на тормоз, но при этом машина (тело) имеет определенную массу и вес, а помимо этого во время торможения имеет еще и скорость. Поэтому, на момент когда водитель затормозил – остановка тела происходит не мгновенно, а своевременно, проехав еще несколько метров. Отношение скорости и массы как раз таки образуют то, что названо "инерцией" в этих примерах.
Второе утверждение – аналогично само по себе простое и легко объясняется. Человек аналогично имеет вес и массу, а во время бега еще и скорость, отсюда мы и получаем, что человек бежит → начинает останавливаться ногами, но при этом, положение тела во время бега (туловище наклонено вперед) делает все само за себя.
Поскольку центр масс во время бега смещен, человек не может мгновенно остановится, а лишь постепенно сбавляет скорость и переходит с бега на шаг. Иначе говоря, тормозить начинают лишь ноги, в то время как туловище все еще находится в движении.
Общее между примерами то, что оба тела подвержены скорости, массе и весу, а поэтому, во время движения и остановки – и на машину, и на человека будет действовать инерция.
:
1)Нам известно, что 1 мм рт. ст. - это 1 метр на земле, надо сделать следующим образом.. . зайти на здание, посмотреть давление, оно должно быть меньше 760 мм рт. ст. , надо от 760 отнять то число, которое получится на высоте здания - это и есть высота здания в метрах!
или
Известно, что при подъеме на высоту 12 метров, давление падает на 1 мм рт ст. Замечаешь давление на земле, поднимаешься на крышу, если давление уменьшилось на 2 мм рт ст, значит высота дома 24 метра. Всё просто.
2)Для этого нужен не только барометр, но и секундомер. Сбросив барометр с крыши здания, секундомером засеките время его падения. Согласно уравнению, описывающему ускоренное движение, путь, пройденный телом в свободном падении, равен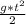 , где g — ускорение свободного падения (9,8 м/с^2), а t — время падения. Вычислив по этой формуле дистанцию, которую пролетел барометр до падения на землю, вы получите высоту здания.
, где g — ускорение свободного падения (9,8 м/с^2), а t — время падения. Вычислив по этой формуле дистанцию, которую пролетел барометр до падения на землю, вы получите высоту здания.
3) Мой любимый - Привяжите барометр к длинной веревке и постепенно спускайте его с крыши здания на землю. Как только барометр коснется земли, измерение завершено. Остается только спуститься на землю и любым измерить длину веревки.