Бесконечная пластина из диэлектрика с проницаемостью ε заряжена однородно с объемной плотностью ρ. Толщина пластины равна 2a. Вне пластины ε=1. Найти: а) поляризованность P диэлектрика как функцию x,
б) поверхностную плотность σ' связанных зарядов на левой (x=-a) и на правой (x=+a) границах пластины,
в) объемную плотность ρ' связанных зарядов.

1) приборы: брусок с разными шириной и высотой; деревянная дощечка длиннее, чем брусок раз в 5; динамометр.

2) положим брусок на дощечку, лежащую на столе.

3) прикрепим к бруску динамометр.

4) будем двигать брусок, тянуть за динамометр. Надо при так, чтобы брусок двигался равномерно хоть 2 секунды. Тогда динамометр покажет силу трения. Они в сумме = 0 и ускорения нет. Стрелка динамометра при этом не дрожит. Не бойтесь увеличить скорость.

5) перевернем брусок на бок. Площадь соприкосновения изменится, а показания динамометра НЕТ.

6) Найдем силу тяжести бруска F=mg, взвесив его на динамометре. Вычислим коэфф. трения

k=Fтр/N=Fтр/mg;  у нас реакция опоры N численно = mg.

Вывод: сила трения и коэффициент трения k=Fтр/N=Fтр/mg не зависят от площади соприкасающихся поверхностей.

Для начала вспомним формулу кинетической энергии:

Е=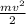

(1) Представим, что мы бросаем этот мяч. Он летит, потом "останавливается" где-то в высшей точке, а потом уже летит вниз. Логично, что если он "останавливается", т.е. не двигается, то и скорость его = 0, следует, по формуле, что кинетическая = 0. ответ 3 верный.

(2) У мяча, пока он летит, скорость не постоянна, иначе как бы он остановился, (так-то еще существуют формулы для свободного падения), значит, что в какой-то момент скорость была наибольшей, а затем начала уменьшаться. Понятно, что скорость максимальна в момент броска. Значит, по формуле кинетическая будет тоже максимальна. ответ 1 неверный.

Неправильность остальных ответов можно объяснить следствиями (2).