Брусок скользит по горизонтальной плоскости. Вычислить ее ускорение в горизонтальной проекции, если на него действует горизонтальная сила F=28 N, его масса m=45 кг и скольжения коэффициент трения между бруском и поверхностью плоскости μ=0,2! Сила поставлена против направления движения, как показано на рисунке.
ответ:На брусок, скользящий по наклонной плоскости, действуют 3 силы: сила тяжести mg, направленная вниз, сила реакции плоскости N, направленная перпендикулярно наклонной плоскости, и сила трения F тр, действующая вдоль наклонной плоскости и направленная в сторону, противоположную движению бруска.
Запишем второй закон Ньютона в проекциях на ось x вдоль наклонной плоскости и на ось y, перпендикулярную наклонной плоскости (брусок имеет некоторое ускорение a, направленное вдоль наклонной плоскости, а в направлении, перпендикулярном наклонной плоскости, ускорение бруска равно 0):
mg sinα – Fтр =ma (1) N – mg cosα =0 (2)
Известно, что сила трения скольжения равна F тр= k N (3)
(где k – это коэффициент трения скольжения).
Решая систему этих трех уравнения, получим
a = g (sinα –k cosα) = 9,8 (1/2 – 0,2 √3/2) = 3,2 м/с в квадрате
сумма сил векторная опр по правилу паралеллограмма, или как там он пишется не помню.
рассмотрим палгрм. со сторонами 6 и 8 и диагональю 4 тогда найдем площадь этой фигуры
у нас есть диагональ можно разложить на два треугольника и по фрмуле горнара вроде найти площадь треугольника,
ы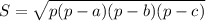
a b c стороны треугольника найдем плщдь треугл. и умножим на два тиак как паралгр. состоит из двух таких тргл.
S = 24 = 8*6* sin L => L = 30 но это угол не тот что мы ищем на рисунке будет видно.
найдем другой угол больший есть 150 грд. искомый угол. он находится так как сумма в четырехугл = 360 то (360 - 30 - 30 )/2 = 150
равнодействующая равно 0 так как люстра висит и не двигается
ответ:На брусок, скользящий по наклонной плоскости, действуют 3 силы: сила тяжести mg, направленная вниз, сила реакции плоскости N, направленная перпендикулярно наклонной плоскости, и сила трения F тр, действующая вдоль наклонной плоскости и направленная в сторону, противоположную движению бруска.
Запишем второй закон Ньютона в проекциях на ось x вдоль наклонной плоскости и на ось y, перпендикулярную наклонной плоскости (брусок имеет некоторое ускорение a, направленное вдоль наклонной плоскости, а в направлении, перпендикулярном наклонной плоскости, ускорение бруска равно 0):
mg sinα – Fтр =ma (1) N – mg cosα =0 (2)
Известно, что сила трения скольжения равна F тр= k N (3)
(где k – это коэффициент трения скольжения).
Решая систему этих трех уравнения, получим
a = g (sinα –k cosα) = 9,8 (1/2 – 0,2 √3/2) = 3,2 м/с в квадрате