Быстро И НУЖНА ОТВЕТ 1. Сила тертя ковзання залежить від а) взаемного розташування тіл, 0) площі стичних тертьових поверхонь,
В) якості тертьових поверхонь, г) відносної швидкості руху тіл.​

я так понимаю, треугольник ABC является абсолютно твёрдым телом?

обозначим единичные векторы направлений сторон e₁, e₂, e₃ (направления AB, BC, AC, соответственно) , а векторы скоростей вершин v₁, v₂, v₃ (вершины A, B, C, соответственно)

в силу нерастяжимости сторон проекции скоростей вершин любой стороны на эту сторону равны, то есть

v₁·e₁=v₂·e₁, v₂·e₂=v₃·e₂, v₃·e₃=v₁·e₃

кроме того из условия следует, что v₂=v e₁ и что v₃=x e₂

векторы e₁, e₂, e₃ единичные, поэтому e₁·e₁=1, e₂·e₂=1, e₃·e₃=1

из геометрии следует, что e₁·e₂=cos 120°=-1/2, e₂·e₃=cos 60°=1/2, e₁·e₃=cos 60°=1/2

подставляя все эти данные в условия нерастяжимости сторон, получим

v₁·e₁=v, -v/2=x, x/2=v₁·e₃

откуда v₁·e₁=v, v₁·e₃=-v/4

пусть v₁=a e₁+b e₃

тогда a+b/2=v, a/2+b=-v/4, откуда a=3v/2, b=-v

v₁²=a²+b²+2ab/2=a²+b²+ab=9v²/4+v²-3v²/2=7v²/4

поэтому |v₁|=(v√7)/2

Дано:

эВ

Согласно уравнению Эйнштейна для фотоэффекта энергия поглощенного кванта hν идет на совершение работы выхода A и на сообщение кинетической энергии вылетевшему электрону: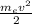

Работа выхода A - это минимальная работа, которую надо совершить, чтобы удалить электрон из металла.

Минимальная частота света v (min), при которой ещё возможен фотоэффект, соответствует максимальной длине волны λmax:

В этой формуле h – это постоянная Планка, равная 6,62·10-³⁴ Дж·с, частоту колебаний можно выразить через скорость света c, которая равна 3·108 м/с, и длину волны по формуле:

Подставим выражение (2) в формулу (1), тогда:

Откуда искомая красная граница фотоэффекта λmax равна:

Посчитаем численный ответ (напоминаем, что 1 эВ = 1,6·10-¹⁹ Дж:

ответ: 0,261 мкм.