Уравнения, которые заданы видом или , являются уравнениями гармонических колебаний. Здесь — координата колеблющегося тела (смещение от положения равновесия); — амплитуда колебаний; — фаза колебаний; — начальная фаза колебаний.
Скорость движения тела, совершающего гармонические колебания, — первая производная координаты от времени:
Ускорение движения тела, совершающего гармонические колебания, — первая производная скорости от времени, вторая производная координаты от времени:
В нашем уравнении имеем:
Кинетическая энергия — физическая величина, которая характеризует механическое состояние движущегося (колеблющегося) тела и равна половине произведения массы тела на квадрат скорости его движения:
Уравнения, которые заданы видом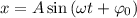
или 
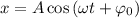, являются уравнениями гармонических колебаний. Здесь 
— координата колеблющегося тела (смещение от положения равновесия);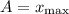 
— амплитуда колебаний; 
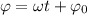— фаза колебаний; 
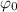— начальная фаза колебаний.
Скорость движения тела, совершающего гармонические колебания, — первая производная координаты от времени: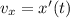
Ускорение движения тела, совершающего гармонические колебания, — первая производная скорости от времени, вторая производная координаты от времени: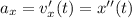
В нашем уравнении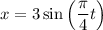
имеем:
Кинетическая энергия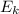
— физическая величина, которая характеризует механическое состояние движущегося (колеблющегося) тела и равна половине произведения массы 
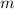тела на квадрат скорости 
его движения:
Для данной задачи имеем:
КПД = 48 %
Объяснение:
дано:
m(глицерин) = 463 г = 463 × 10^(-3) кг
m(бензин) = 3,1 г = 3,1 × 10^(-3) кг
t1 = 22 C
t2 = 84 C
c = 2400 Дж / (кг × С)
q = 46 MДж/кг = 46 × 10^6 Дж /кг
найти:
КПД
Q(нагревание) = c × m(глицерин) × (t2 - t1)
Q(сгорание) = q × m(бензин)
КПД = ( Q(нагревание) / Q(сгорание) ) × 100%
общая формула:
КПД = ( (c × m(глицерин) × (t2 - t1)) / q × m(бензин) ) × 100%
подставим значения:
КПД = ( (2400 × 463 × 10^(-3) × (84 - 22)) / (46 × 10^6 × 3,1 × 10^(-3)) ) × 100% = ( (68894,4 / (142,6 × 10^3) ) × 100% = 0,48 × 100% = 48 %