Если мне не изменяет память, недавно просматривали свою коллекцию животных мира, так там был один фильм про гепардов. И было озвучено, что скорость этой дикой кошечки достигает 120 км в час. Если не ошибаюсь он и является самым быстроходным животным из линейки существующих млекопитающих, которые топчут в современном мире нашу бедную землю-матушку-). Если вы конечно животных имели ввиду-)P.S. А если людей брать в расчет, то думаю пока еще ямайского бегуна-спринтера Усейна Болта невозможно в скорости переплюнуть, просто кудесник на своих 100 и 200 метрах (это я на всякий случай добавляю, вдруг тег - "живые существа" подразумевает именно такую постановку вопроса-)
Если решать эту задачу по школьному, без привлечения инструментария матанализа, то рассуждать можно следующим образом, - в любой точке траектории ускорение свободного падения может быть разложено на две составляющих - вдоль касательной к траектории (нормальное ускорение) и вдоль нормали к траектории (центростремительное ускорение), нам нужна вторая величина, так как она позволяет рассчитать искомый радиус. В наивысшей точке подъема мяча, очевидно, что центростремительное ускорение целиком совпадает с ускорением свободного падения:
Откуда:
Горизонтальная составляющая скорости будет везде одинакова и равна (учтем что 54 км/ч=15 м/с):
11,25 м
Объяснение:
Если решать эту задачу по школьному, без привлечения инструментария матанализа, то рассуждать можно следующим образом, - в любой точке траектории ускорение свободного падения может быть разложено на две составляющих - вдоль касательной к траектории (нормальное ускорение) и вдоль нормали к траектории (центростремительное ускорение), нам нужна вторая величина, так как она позволяет рассчитать искомый радиус. В наивысшей точке подъема мяча, очевидно, что центростремительное ускорение целиком совпадает с ускорением свободного падения:
Откуда:
Горизонтальная составляющая скорости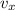
будет везде одинакова и равна (учтем что 54 км/ч=15 м/с):
Искомый радиус кривизны траектории: