Температуры сосудов постоянны и поддерживаются внешней средой, значит воздух после открытия крана как-то перемешается, но его температура через какое-то время станет равной температуре внешней среды, т.е. в конечном счете воздуха в сосудах не меняются. Меняется лишь давление, оно будет одинаковым в каждом сосуде.
Пренебрегая наличием воздуха в капилляре (ведь в действительности какая-то часть воздуха всегда будет находиться в этой тонкой трубке и иметь некую промежуточную температуру между и ) можно написать
где все соотв. кол-ву воздуха в первом/втором сосуде до/после открытия крана. Используя (#), это равенство можно переписать как
Кубик может подпрыгнуть, если модуль силы F¯, действующей на него со стороны пули, окажется большим модуля силы тяжести Mg=1Н .Найдем эту силу. Для этого рассмотрим пулю. На нее со стороны кубика действует такая же по модулю, но противоположная по направлению сила и сила тяжести mg.
Скорость пули при пролете сквозь кубик меняется незначительно: ее изменение равно 5м/с, что составляет всего 5% от скорости пули при входе в кубик. Поэтому можно считать, что сила F¯ не зависит от скорости пули и постоянна.
Импульс пули при пролете сквозь кубик меняется благодаря действию на пулю двух сил - силы тяжести и силы трения.
Если время, за которое пуля пролетает сквозь кубик, обозначить через τ, то m(v1−v2)=(F+mg)τ. (1)
Время τ найти нетрудно. Так как силы, действующие на кубик, постоянны, то постоянно и ускорение пули, а значит, скорость пули меняется со временем линейно.
Поэтому средняя скорость движения пули в кубике равна
vср=v1+v22
. Следовательно, пуля пролетает сквозь кубик за время τ=hvср=2av1+v2≈10−3с
Подставив это значение τ в формулу (1), найдем:
F=m(v1−v2)−μgττ≈50НF Так как τ мало, то величина mgτ много меньше изменении импульса пули и ею можно пренебречь. Сила F оказалась больше силы тяжести, которая действует на кубик. Поэтому кубик подскочит.
Уравнение состояния идеального газа выглядит как
Температуры сосудов постоянны и поддерживаются внешней средой, значит воздух после открытия крана как-то перемешается, но его температура через какое-то время станет равной температуре внешней среды, т.е. в конечном счете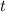
воздуха в сосудах не меняются. Меняется лишь давление, оно будет одинаковым в каждом сосуде.
Пренебрегая наличием воздуха в капилляре (ведь в действительности какая-то часть воздуха всегда будет находиться в этой тонкой трубке и иметь некую промежуточную температуру между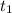
и 
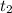) можно написать
где все
соотв. кол-ву воздуха в первом/втором сосуде до/после открытия крана. Используя (#), это равенство можно переписать как
откуда
Кубик может подпрыгнуть, если модуль силы F¯, действующей на него со стороны пули, окажется большим модуля силы тяжести Mg=1Н .Найдем эту силу. Для этого рассмотрим пулю. На нее со стороны кубика действует такая же по модулю, но противоположная по направлению сила и сила тяжести mg.
Скорость пули при пролете сквозь кубик меняется незначительно: ее изменение равно 5м/с, что составляет всего 5% от скорости пули при входе в кубик. Поэтому можно считать, что сила F¯ не зависит от скорости пули и постоянна.
Импульс пули при пролете сквозь кубик меняется благодаря действию на пулю двух сил - силы тяжести и силы трения.
Если время, за которое пуля пролетает сквозь кубик, обозначить через τ, то m(v1−v2)=(F+mg)τ. (1)
Время τ найти нетрудно. Так как силы, действующие на кубик, постоянны, то постоянно и ускорение пули, а значит, скорость пули меняется со временем линейно.
Поэтому средняя скорость движения пули в кубике равна
vср=v1+v22
. Следовательно, пуля пролетает сквозь кубик за время τ=hvср=2av1+v2≈10−3с
Подставив это значение τ в формулу (1), найдем:
F=m(v1−v2)−μgττ≈50НF Так как τ мало, то величина mgτ много меньше изменении импульса пули и ею можно пренебречь. Сила F оказалась больше силы тяжести, которая действует на кубик. Поэтому кубик подскочит.