Что произойдет при столкновении двух одинаковых по массе пластилиновых шаров, движущихся навстречу друг другу с одинаковыми по модулю скоростями?

Показать ответ

Ответ:

ololol1213

02.09.2021 00:10

Объяснение:

1.Обозначим токи и составим ур:

I3-I2-I5=0

E3+E1-E2=I3R3+I2R2+I2R1

E3+E5+E4=I3R3+I5R5+I5R4 подставим значения

30+10-20=I3R3+I(R2+R1), 20=45I3+30I2 (5) сократим коэф.на 5

30+50+40=I3R3+I5(R5+R4), 120=45I3+150I2

4=9I3+6I2 (1) в ур.1 и 2 выразим ток I3 через I2+I5.

25=9I3+30I5 (2)

I2+I5=I3 4=9(I2+I5)+6I2

25=9(I2+I5)+30I5 умножив и сложив подобные:

4=15I2+9I5 (3)

25=9I2+39I5 (4) из ур.3 ищем ток I2=4-9I5/15, подставим в ур.4, получ.

25=9(4-9I5)/15 +39I5< сократим 9 и 15на 3, общий знам.5, получим:

125=12-27I5+195I5 ⇒113=168I5 ⇒I5=0.6726a

I2=4-9*0.6726/15= -0.1369a

I3= -0.1369+0.6726=0.5357a подставив токи в ф-лу (5)убеждаемся в правильности решения

0,0(0 оценок)

Ответ:

Tori163

30.06.2022 17:23

$T = \frac{2}{r} \sqrt{ \frac{ \pi m }{ \rho g } } = 3.98$ сек = 4 с .

Объяснение:

$r=1.5 \cdot 10^{-3}$ м – радиус окружности сечения ареометра.

$s = \pi r^2$ – площадь сечения ареометра.

$m=2.5 \cdot 10^{-2}$ кг – масса ареометра.

$\rho = 900$ кг/м³ – плотность жидкости.

Ось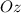 – направлена вертикально вниз.

Выберем ноль для вертикальной Оси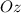 , напротив положения нижней точки ареометра, когда тот находится в состоянии равновесия.

Колебания потенциальной энергии жидкости мы будем учитывать (в Энергетическом Решении), т.е. изменение общего объёма "жидкость и погружённая часть ареометра". Однако, моменты увеличения и уменьшения указанного объёма мы будем считать происходящими на фоне пренебрежимо малых изменений высоты жидкости, считая площадь поверхности жидкости достаточно большой. Короче говоря, колебаниями уровня жидкости мы пренебрегаем, поскольку нам не сообщается не только площадь сечения сосуда, а, да и вообще ничего о его форме, которая может иметь даже переменную по высоте площадь сечения. Так что приходится просто считать, что сечение сосуда, в основном, многократно больше по площади, чем сечение ареометра, а стало быть, его погружение в сосуд не влияет на уровень жидкости в сосуде так, чтобы нам приходилось бы вследствие этого значительно пересчитывать координату ареометра.

ДИНАМИЧЕКОЕ РЕШЕНИЕ:

По закону Архимеда:

$F_{apx} = \rho g s h$ , где – высота погружённой части ареометра в любой момент,

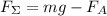h = h_o + z , где h_o – высота погружённой части ареометра в состоянии равновесия.

Вообще: $F_\Sigma = mg-F_A$ ;

В состоянии равновесия:

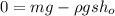(*) $0 = mg-\rho g s h_o$ ;

В любой момент:

$F_\Sigma = mg - \rho g s h_o - \rho g s z$ ;

$F_\Sigma = - \rho g s z$ ;

Разделим на массу:

$\frac{F_\Sigma}{m} = - \frac{\rho g s z}{m}$ ;

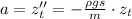(**) $a = z''_t = - \frac{\rho g s}{m} \cdot z_t$ ;

Получаем классическое дифференциальное уравнение с гармоническим решением:

$z = A \cos{ \omega t }$ , где $\omega = \sqrt{ \frac{\rho g \pi r^2}{m} } = r \sqrt{ \frac{\rho g \pi }{m} }$ ;

$T = \frac{ 2 \pi }{\omega} = \frac{2}{r} \sqrt{ \frac{ \pi m }{ \rho g } }$ ;

ЭНЕРГЕТИЧЕСКОЕ РЕШЕНИЕ:

Нужно учесть энергию подъёма жидкости.

Когда ареометр погружается из состояния равновесия на глубину , он вымещает из-под себя дополнительный объём жидкости 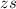, который перемещается от своего центра масс, находившегося на координате 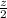$\frac{z}{2}$ до новой координаты 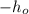-h_o , "размазываясь" по поверхности жидкости. Увеличение потенциальной энергии жидкости при этом составляет:

$zs\rho g ( h_o + \frac{z}{2} )$ ;

Уменьшение потенциальной энергии самого ареометра при этом составляет:

mgz ;

Общее увеличение потенциальной энергии системы "жидкость и ареометр":

$zs\rho g ( h_o + \frac{z}{2} ) - mgz = \frac{s\rho gz^2}{2} + zs\rho g h_o - mgz = \frac{s\rho gz^2}{2} + z ( s\rho g h_o - mg )$ ;

Заметив, что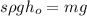 $s\rho g h_o = mg$ , как это следует из уравнения равновесия (*), имеем общее увеличение потенциальной энергии системы "жидкость и ареометр" в упрощённом виде:

$\frac{s\rho gz^2}{2}$ , при этом в процессе малых колебаний, ареометр имеет и какую-то кинетическую энергию $\frac{mv^2}{2}$ , в сумме с которой мы будем иметь полную сохраняющуюся механическую энергию:

$\frac{s\rho gz^2}{2} + \frac{mv^2}{2} = const$ , продифференцируем:

$s\rho gzv + mva = 0$ , поделим на скорость:

$s\rho gz + ma = 0$ ,

$a = z''_t = -\frac{ s\rho g }{m} \cdot z_t$ , и вот мы опять пришли к уравнению (**), решение которого уже произведено.

ОКОНЧАТЕЛЬНО:

$T = \frac{2}{r} \sqrt{ \frac{ \pi m}{ \rho g } } = \frac{2}{ 1.5 \cdot 10^{-3}} \sqrt{ \frac{ \pi \cdot 2.5 \cdot 10^{-2}}{ 900 \cdot 9.8 } }$ сек $= \frac{4000}{3} \sqrt{ \frac{25 \pi \cdot 10^{-4}}{9 \cdot 98 } }$ сек $= \frac{20 \cdot 5 \sqrt{ 2 \pi } }{3 \cdot 3 \cdot 7 }$ сек $= \frac{100 \sqrt{ 2\pi }}{63}$ сек = 3.98 сек = 4 с .