ответ: 11 КДж.
Объяснение:
Дано:
c1(серебра) = 250 Дж/(кг·°С).
c2(подсолнечного масла) = 1700 250 Дж/(кг·°С)
m1 = 200 г = 0.2 кг.
m2 = 100 г = 0.1 кг.
t0=20°С
t=70°С
Найти:
Q1+Q2-?
Q=cmΔt
Тобишь нам надо найти кол-во теплоты необходимое для нагревания емкости и самого масла.
Обозначим теплоту, необходимую для нагревания емкости Q1, а самого масла Q2.
Начнем с Q1.
Удельная теплоемкость серебра - 250 Дж/(кг·°С).
200 г = 0.2 кг.
Q1=250*0.2*(70-20)=250*0.2*50=2500 Дж.
Перейдем к Q2.
Удельная теплоемкость подсолнечного масла - 1700 Дж/(кг·°С).
100 г = 0.1 кг.
Q2=1700*0,1*(70-20)=1700*0.1*50=8500 Дж.
Q=Q1+Q2
Q=2500+8500= 11000 Дж = 11 КДж.
Должно получится так.
В ;
А ;
Вт ;
Вт.
Токи через , и равны, как неразветвляющиеся: А ;
Мощности на , и равны, соответственно:
Вт Вт ;
Напряжения на , и равны, соответственно:
В В ;
Общее напряжение на и участке, состоящем из , и равны, как параллельно подключённые:
В
Мощность на равна:
Ток через по закону Ома:
А А ;
Токи через и , как, соответственно, разветвляющийся и стекающийся, находятся суммированием токов через и через участок, состоящий из , и :
Мощности на и равны, соответственно:
Вт
Напряжения на и равны, соответственно:
Общее напряжение на и участке, состоящем из , и (с распараллеливанием) равны, как параллельно подключённые:
Общий ток, как разветвляющийся:
А А А ;
Общая мощность:
Вт Вт Вт ;
Баланс мощности:
;
.
ответ: 11 КДж.
Объяснение:
Дано:
c1(серебра) = 250 Дж/(кг·°С).
c2(подсолнечного масла) = 1700 250 Дж/(кг·°С)
m1 = 200 г = 0.2 кг.
m2 = 100 г = 0.1 кг.
t0=20°С
t=70°С
Найти:
Q1+Q2-?
Q=cmΔt
Тобишь нам надо найти кол-во теплоты необходимое для нагревания емкости и самого масла.
Обозначим теплоту, необходимую для нагревания емкости Q1, а самого масла Q2.
Начнем с Q1.
Удельная теплоемкость серебра - 250 Дж/(кг·°С).
200 г = 0.2 кг.
Q1=250*0.2*(70-20)=250*0.2*50=2500 Дж.
Перейдем к Q2.
Удельная теплоемкость подсолнечного масла - 1700 Дж/(кг·°С).
100 г = 0.1 кг.
Q2=1700*0,1*(70-20)=1700*0.1*50=8500 Дж.
Q=Q1+Q2
Q=2500+8500= 11000 Дж = 11 КДж.
ответ: 11 КДж.
Должно получится так.
Объяснение:
Токи через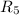 ,
, 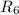 и
и 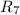 равны, как неразветвляющиеся:
равны, как неразветвляющиеся: 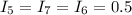 А ;
А ;
Мощности на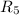 ,
, 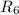 и
и 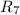 равны, соответственно:
равны, соответственно:
Напряжения на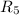 ,
, 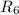 и
и 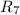 равны, соответственно:
равны, соответственно:
Общее напряжение на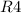 и участке, состоящем из
и участке, состоящем из 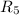 ,
, 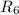 и
и 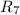 равны, как параллельно подключённые:
равны, как параллельно подключённые:
Мощность на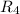 равна:
равна:
Ток через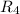 по закону Ома:
по закону Ома:
Токи через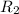 и
и 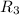 , как, соответственно, разветвляющийся и стекающийся, находятся суммированием токов через
, как, соответственно, разветвляющийся и стекающийся, находятся суммированием токов через 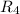 и через участок, состоящий из
и через участок, состоящий из 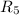 ,
, 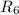 и
и 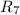 :
:
Мощности на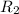 и
и 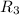 равны, соответственно:
равны, соответственно:
Напряжения на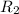 и
и 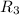 равны, соответственно:
равны, соответственно:
Общее напряжение на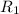 и участке, состоящем из
и участке, состоящем из 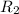 ,
, 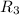 и
и 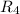 (с распараллеливанием) равны, как параллельно подключённые:
(с распараллеливанием) равны, как параллельно подключённые:
Мощность на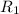 равна:
равна:
Ток через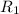 по закону Ома:
по закону Ома:
Общий ток, как разветвляющийся:
Общая мощность:
Баланс мощности: