Внимательно посмотрим на два основных типа блока: подвижный и неподвижный (см. рисунок).
Для неподвижного блока груз поднимается под действием силы натяжения веревки Т на высоту h, в то же время, другой конец веревки опускается на расстояние h под действием силы F, равной T, их работы:
Но так как то и работы этих сил равны между собой.
Для подвижного блока груз поднимается на высоту h под действием силы натяжения веревки Т, но другой конец вытягивается на 2h за счет вдвое меньшей силы, сравним их работы:
Пришли к тому же результату, т.е. и подвижный блок не дает выигрыша в работе.
На самом деле отсутствие выигрыша в работе является следствием золотого правила механики: Во сколько раз мы выигрываем в силе, во столько же раз проигрываем в расстоянии, а работа, как произведение этих двух величин, никак не меняется.
Более того, в реальных механизмах, полезная работа всегда оказывается меньше затраченной из-за наличия силы трения и т.д. Поэтому КПД реальных механизмов всегда меньше 1.
Внимательно посмотрим на два основных типа блока: подвижный и неподвижный (см. рисунок).
Для неподвижного блока груз поднимается под действием силы натяжения веревки Т на высоту h, в то же время, другой конец веревки опускается на расстояние h под действием силы F, равной T, их работы:
Но так как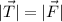
то и работы этих сил равны между собой.
Для подвижного блока груз поднимается на высоту h под действием силы натяжения веревки Т, но другой конец вытягивается на 2h за счет вдвое меньшей силы, сравним их работы:
Пришли к тому же результату, т.е. и подвижный блок не дает выигрыша в работе.
На самом деле отсутствие выигрыша в работе является следствием золотого правила механики: Во сколько раз мы выигрываем в силе, во столько же раз проигрываем в расстоянии, а работа, как произведение этих двух величин, никак не меняется.
Более того, в реальных механизмах, полезная работа всегда оказывается меньше затраченной из-за наличия силы трения и т.д. Поэтому КПД реальных механизмов всегда меньше 1.
ответ: 41 м
Объяснение:
Дано:
h = 5 м
α = 30°
μ = 0,1
s - ?
Согласно ЗСЭ при движении санок по наклонной плоскости
mgh = ( mv² )/2 + Aтр.1
Где Aтр.1 - работа сил трения на наклонной плоскости
v - скорость тела у "подножия" наклонной плоскости
Поэтому
Атр.1 = Fтр.1L
Где L - длина наклонной плоскости
Атр.1 = μN1L
Т.к. N1 = mgcosα ( Докажите самостоятельно )
Тогда
Атр.1 = μmgcosαL
Возвращаюсь к начальному уравнению
Получим что
mgh = ( mv² )/2 + μmgcosαL (1)
Теперь перейдем к движению тела на горизонтальной плоскости
Согласно ЗСЭ
( mv² )/2 = Aтр.
( mv² )/2 = Fтр.s
Где Fтр. - сила трения на горизонтальном участке движения
Соответственно Fтр. = μmg ( Докажите самостоятельно )
Тогда
( mv² )/2 = μmgs
Подставим данное выражение в уравнение (1)
mgh = μmgs + μmgcosαL
У Отсюда
L = h/sinα
Тогда
h = μ( s + ( hcosα )/sinα )
h = μ( s + hctgα )
s + hctgα = h/μ
s = h/μ - hctgα
s = h( 1/μ - ctgα )
s = 5( 1/0,1 - 1,73 ) ≈ 41 м
Объяснение:
точно не знаю но вроде бы так!!