Диск массой m=7кг и радиусом R=0,1 м начинает катиться без скольжения вверх по наклонной плоскости с углом наклона к горизонту а=40°. Найти высоту, на которую он пдниметься при начальной скорости Vo=5 м/c g=9,8

Показать ответ

Ответ:

Ellionora1227

05.01.2023 11:56

Объяснение:

Начнем с того, что кинетическая энергия находится по формуле

Eк =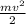 $\frac{mv^2}{2}$

Из этой формулы нам надо выразить квадрат скорости. Но для начала мы Eк домножим на два.

Получим уравнение:

2Eк = mv^2 (^2 - степень числа)

Выразим из этого уравнения квадрат скорости.

v^2 =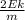 $\frac{2Ek}{m}$

Подставим величины в формулу:

v^2 =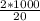 $\frac{2 * 1000}{20}$

v^2 = 100

А теперь вопрос: вы хоть раз слышали что-то о квадратных корнях?

Так вот, квадратные корни вы будете проходить по алгебре в 8 классе. Извлечение квадратного корня(в нашем случае - арифметического) - это такое неотрицательное число, которое в нашем случае при возведении в квадрат даст 100.

То есть,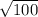 $\sqrt{100}$ = 10 м/с

То есть, скорость тела равна 10 м/с.

Задача решена.

0,0(0 оценок)

Ответ:

kotena555

04.10.2020 12:10

Вторая космическая скорость (параболическая скорость, скорость убегания) - наименьшая скорость, которую необходимо придать объекту (например, космическому аппарату), масса которого пренебрежимо мала по сравнению с массой небесного тела (например, планеты), для преодоления гравитационного притяжения этого небесного тела и покидания замкнутой орбиты вокруг него.

$\displaystyle v_{2}=\sqrt{2G\cdot\frac{M_{n}}{R_{n}} }$

где G = 6,67·10⁻¹¹ (Hм²/кг²) - гравитационная постоянная

M(n) - масса планеты (кг)

R(n) = R(з)/2 - радиус планеты (м)

Определим массу планеты:

$\displaystyle M_{n}=\rho_{n}V_{n}=\frac{1}{3}\cdot5,5\cdot10^{3}\cdot\frac{4}{3}\cdot3,14\cdot\bigg(\frac{6,37\cdot10^{6}}{2}\bigg)^{3}=\\\\\\{} \ \ \ \ \ \approx7,68\cdot10^{3}\cdot32,3\cdot10^{18}=2,48\cdot10^{23} \ (kr)$

Вторая космическая скорость для планеты:

$\displaystyle v_{2}=\sqrt{2\cdot6,67\cdot10^{-11}\cdot\frac{2,48\cdot10^{23}}{3,185\cdot10^{6}}}=\sqrt{10,39\cdot10^{6}}\approx3.2\cdot10^{3} \ (m/c)$