Диск радиусом R = 0,6 м вращается вокруг неподвижной оси так, что зависимость его углового ускорения от времени задается уравнением E(эпсилон) =At, где A =3 рад/с'3 . Определите угол (фи) поворота диска за время t = 2,2 с после начала
движения, линейную скорость точки v на ободе диска и ее нормальное ускорение an для этого же момента времени.
1) Чтобы найти силу упругости, достаточно воспользоваться формулой F=mg, где F - сила упругости, m - масса груза, g - ускорение свободного падения. Допустим, что g=10м/c2
Найдем F: 6 кг * 10 = 60 Н.
ответ: 60 Н
2) Чтобы найти жесткость пружины, применим формулу: F=kx, где F - сила упругости, k - коэффициент жесткости пружины, x - удлинение или сжатие пружины. Нам нужно k. Выразим его: k=F/x.
Найдем k: 60 / 4 = 15 Н/м.
ответ: 15 Н/м
3) Формула потенциальной энергии пружины: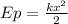
Подставляем уже известные циферки: Еп=15*4^2/2=240/2=120 Дж
Вот и ответ: 120 Дж
А-
Дано: V = 600 м/c, m = 0,0075 кг
Найти: Eк - ?
больно щедро за такую задачу) Будем искать кинетическую энергию по формуле:
E = \frac{mV^{2}}{2} = \frac{0,0075*360.000}{2} = \frac{2700}{2} = 1350 Дж = 1,35 кДж
ответ: 1350 Дж или 1,35 кДж
Б-
Расчет по формуле потенциальной энергии: Ep = mgh
g= 9,8 Н/м
Е=50*20*9,8
Е=9800Дж
С-
Правило рычага F1 / F2 = L2 /L1 или 10 /100 = 2 / L1, L1 =2 x100 / 10 = 20 cm
Д-
Минимальная необходимая сила расчитывается из условия равенства моментов:
FL1 = mgL2
F = mgL2/L1 = 2000 *0,5/2 = 500 Н.
ответ: 500 Н.