*** если же переход от наклонной плоскости скруглённый, и: , то:
.
Объяснение:
По закону сохранений энергии:
;
где:
и – начальные значения кинетической и потенциальной энергии;
и – значения кинетической и потенциальной энергии перед ударом о горизонтальную поверхность, в самом низу наклонной плоскости;
– работа силы трения на наклонной плоскости;
– работа
силы трения на наклонной плоскости,
где: – длина наклонной плоскости;
;
В итоге:
;
(*) ;
Из этого вытекает очевидное условие, что:
;
;
, т.е. угол наклона должен быть более значения: , иначе груз вообще не сдвинется с места, и, разумеется, никакого расстояния не пройдёт, а общая формула (данная в ответе) даст формально отрицательный ответ для высоты .
Теперь «удар», т.е. переход с наклонной плоскости на горизонталь. Во время удара теряется вертикальная составляющая импульса . Это происходит почти мгновенно ( ), под воздействием гасящей его чрезвычайно резко возрастающей на время гашения силы реакции опоры (и веса – соответственно) . Удар груза об опору в момент его перехода на горизонталь будем считать абсолютно неупругим, происходящим таким образом, что груз после него не подскакивает. Тогда можно записать, что:
;
;
За это время груз так же заметно замедляется под воздействием чрезвычайно резко возрастающей на время гашения силы трения:
;
Соответственно, гасится и горизонтальный импульс:
;
;
Из последнего вытекает очевидное условие, что:
;
;
;
, т.е. угол наклона должен быть не более определённого значения: , иначе груз после удара о горизонтальную плоскость просто остановится, и никакого расстояния не пройдёт, а общая формула (данная в ответе) даст формально отрицательный ответ для высоты .
Кинетическая энергия груза после «ударного» торможения:
;
Далее, снова по закону сохранений энергии (с учётом неизменного значения потенциальной):
;
где:
– работа силы трения на горизонтальном участке до остановки;
а – конечная кинетическая энергия (остановка);
;
;
Учитывая (*):
;
;
.
*** Если же переход от наклонной плоскости гладкий, и при этом: , т.е. радиус перехода: , то «ударная» потеря – пренебрежима, и: , а, значит:
1)Моторная лодка движется от носа теплохода длинной 36 метров и обратно с постоянной скоростью за 2 мин. Скорость теплохода 9 км/ч. Определить скорость лодки решение t= t1+t2 t1=L/(V1-V2) V2=9 км/ч=2,5 м/с t2=L/(V1+V2) 120=36/(V1-2,5)+36/(V1+2,5) V1=X после преобразований получаем 10*x^2-6*x -62,5=0 x=2,8 2м/с
2) Автомобиль за проходит первую треть пути с некоторой постоянной скоростью, а оставшуюся часть пути со скоростью 72км/ч. Определите скорость движения автомобиля на первом участке, если его средняя скорость на всем пути равна 54км/ч. Vср=S/t=S/(t1+t2)=S/(S/3*V1 +2*S/3*V2)=3/(1/V1+2/V2) Vcр=3*V1*V2/(V2+2*V1) 54=3*X*72/(72+2*X) X=36 км/ч=10 м/с
3) В отсутствие ветра парашютист опускается на землю со скоростью 4м/с. С какой скоростью он будет двигаться при горизонтальном ветре, скорость ветра равна 3м/с
*** если же переход от наклонной плоскости скруглённый, и: , то:
, то:
Объяснение:
По закону сохранений энергии:
где:
силы трения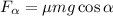 на наклонной плоскости,
на наклонной плоскости,
где: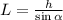 – длина наклонной плоскости;
– длина наклонной плоскости;
В итоге:
(*)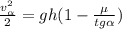 ;
;
Из этого вытекает очевидное условие, что:
Теперь «удар», т.е. переход с наклонной плоскости на горизонталь. Во время удара теряется вертикальная составляющая импульса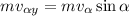 . Это происходит почти мгновенно (
. Это происходит почти мгновенно ( 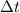 ), под воздействием гасящей его чрезвычайно резко возрастающей на время гашения силы реакции опоры (и веса – соответственно)
), под воздействием гасящей его чрезвычайно резко возрастающей на время гашения силы реакции опоры (и веса – соответственно)  . Удар груза об опору в момент его перехода на горизонталь будем считать абсолютно неупругим, происходящим таким образом, что груз после него не подскакивает. Тогда можно записать, что:
. Удар груза об опору в момент его перехода на горизонталь будем считать абсолютно неупругим, происходящим таким образом, что груз после него не подскакивает. Тогда можно записать, что:
За это время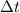 груз так же заметно замедляется под воздействием чрезвычайно резко возрастающей на время гашения силы трения:
груз так же заметно замедляется под воздействием чрезвычайно резко возрастающей на время гашения силы трения:
Соответственно, гасится и горизонтальный импульс:
Из последнего вытекает очевидное условие, что:
Кинетическая энергия груза после «ударного» торможения:
Далее, снова по закону сохранений энергии (с учётом неизменного значения потенциальной):
где:
а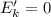 – конечная кинетическая энергия (остановка);
– конечная кинетическая энергия (остановка);
Учитывая (*):
*** Если же переход от наклонной плоскости гладкий, и при этом: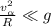 , т.е. радиус перехода:
, т.е. радиус перехода:  , то «ударная» потеря – пренебрежима, и:
, то «ударная» потеря – пренебрежима, и: 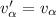 , а, значит:
, а, значит:
решение
t= t1+t2 t1=L/(V1-V2) V2=9 км/ч=2,5 м/с
t2=L/(V1+V2)
120=36/(V1-2,5)+36/(V1+2,5) V1=X
после преобразований получаем
10*x^2-6*x -62,5=0
x=2,8 2м/с
2) Автомобиль за проходит первую треть пути с некоторой постоянной скоростью, а оставшуюся часть пути со скоростью 72км/ч. Определите скорость движения автомобиля на первом участке, если его средняя скорость на всем пути равна 54км/ч.
Vср=S/t=S/(t1+t2)=S/(S/3*V1 +2*S/3*V2)=3/(1/V1+2/V2)
Vcр=3*V1*V2/(V2+2*V1)
54=3*X*72/(72+2*X)
X=36 км/ч=10 м/с
3) В отсутствие ветра парашютист опускается на землю со скоростью 4м/с. С какой скоростью он будет двигаться при горизонтальном ветре, скорость ветра равна 3м/с
скорости складываются как вектора
V=√V1²+V2²=√25=5 м/с - ответ