Дві не пружні тіла масою 2 і 6 кг рухаються назустріч одне одному зі швидкістю кожне. З якою швидкістю і в який бік рухатимуться ці тіла після удару ?
По закону всемирного тяготения сила взаимодействия
1) , где — масса Земли, — масса Луны, — радиус орбиты Луны.
С другой стороны, Луна движется только с центростремительным ускорением, значит по II закону Ньютона
2) , где — центростремительное ускорение;
3) , где — угловая скорость;
4) , где — период обращения Луны вокруг Земли;
5)
6)
Тогда
7)
8)
К слову, масса Земли, которая фигурирует в последней формуле, была вычислена в 1798 году Генри Кавендишем на основе уже известного в то время радиуса Земли. Радиус же Земли был вычислен опытным путём в 240 году до нашей эры Эратосфеном Киренским. Поэтому предлагаю перейти в нашей формуле от массы Земли к радиусу Земли. Мы знаем, что тело на поверхности Земли движется с ускорением , и на основе вышеизложенного можем написать аналогичное уравнение
молекула-этл мельчайшая частица данного вещества
#2
преремещаясь из одного песта в другое тоюело движется по линии
#3путь разделить на промежуток ремени
#4 непрерывно ьепорядочно
#5 частица из которых состоит молекул
#6русский химик
#7плавление нагревание отвердевание
#8
#9взаимное
#10 в твёрдом жидком и газообразном
#11 опытами
#12неделимыми вроде но не уверена
#13 теплой потом горячей
#14
#15демокрит
#16 взаимное проникновение соприкасающиз
#17 термометром
#18
#19 расстояние большое и почти не притягиваются.
#20 не имеют постоянного объёма и формы
По закону всемирного тяготения сила взаимодействия
1)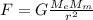 , где
, где 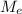 — масса Земли,
— масса Земли, 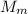 — масса Луны,
— масса Луны,  — радиус орбиты Луны.
— радиус орбиты Луны.
С другой стороны, Луна движется только с центростремительным ускорением, значит по II закону Ньютона
2)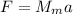 , где
, где  — центростремительное ускорение;
— центростремительное ускорение;
3)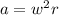 , где
, где 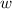 — угловая скорость;
— угловая скорость;
4)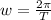 , где
, где 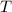 — период обращения Луны вокруг Земли;
— период обращения Луны вокруг Земли;
5)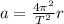
6)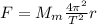
Тогда
7)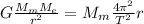
8)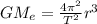
К слову, масса Земли, которая фигурирует в последней формуле, была вычислена в 1798 году Генри Кавендишем на основе уже известного в то время радиуса Земли. Радиус же Земли был вычислен опытным путём в 240 году до нашей эры Эратосфеном Киренским. Поэтому предлагаю перейти в нашей формуле от массы Земли к радиусу Земли. Мы знаем, что тело на поверхности Земли движется с ускорением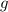 , и на основе вышеизложенного можем написать аналогичное уравнение
, и на основе вышеизложенного можем написать аналогичное уравнение
9)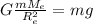 , где
, где 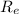 — радиус Земли;
— радиус Земли;
10)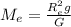
Подставим массу Земли в формулу 8.