Два одинаковых маленьких бруска массами m = 0,6 кг каждый легкой пружиной и положили на наклонную образующую угол α = 30 ° с горизонтом, так, как показано на рисунке. коэффициент трения между брусками и плоскостью равен μ = 0,8 . при какой максимальной деформации ∆x пружины эта система может находиться в покое? считайте, что g = 10 м/с2. соединили друг жёсткостью с другом k = 80 н/м плоскость,
Дано:
============================
Найти: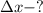
============================
Решение. Рассмотрим один из двух маленьких брусков, так как они одинаковые. На брусок действуют три силы: сила тяжести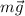 , сила трения
, сила трения 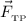 и сила упругости
и сила упругости 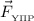 (см. рисунок).
(см. рисунок).
Свяжем систему координат с бруском на поверхности Земли, ось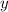 направим перпендикулярно поверхности плоскости, ось
направим перпендикулярно поверхности плоскости, ось  — вдоль поверхности (при таком выборе осей только одна сила
— вдоль поверхности (при таком выборе осей только одна сила 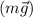 не лежит на осях координат).
не лежит на осях координат).
Если два бруска покоятся, то сложим геометрически эти три силы и приравняем их к нулю:
Спроецируем уравнение на оси координат (сила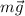 не лежит на оси координат, поэтому для нахождения её проекций опустим из конца вектора
не лежит на оси координат, поэтому для нахождения её проекций опустим из конца вектора 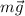 перпендикуляры на оси
перпендикуляры на оси  и
и 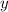 :
: 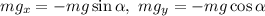 ) и запишем выражения для силы трения
) и запишем выражения для силы трения 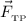 :
:
Распишем все силы, действующие на брусок:
Подставим их в уравнение:
Определим значение искомой величины:
============================
ответ: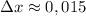 м
м