Два стальных шарика массами m1= 2,5 кг и m2= 2,2 кг движутся по гладкой горизонтальной поверхности вдоль одной прямой друг за другом (первый за вторым) со скоростями v1= 9 м/с и v2= 2 м/с соответственно. После столкновения шаров происходит упругий удар, в результате которого скорость первого шара уменьшается на Δv= 2 м/с, и шарики раскатываются в разные стороны. Определи скорость второго шарика после столкновения. (ответ округли до десятых.) Шаг 1. Найди импульс первого шарика до взаимодействия:
Шаг 2. Найди импульс второго шарика до взаимодействия
Шаг 3. Найди суммарный импульс двух шариков до взаимодействия, учитывая, что шарики движутся друг за другом (первый за вторым)
Шаг 4. Найди скорость первого шарика после взаимодействия
Шаг 5. Найди импульс первого шарика после взаимодействия:
Шаг 6. Обозначив скорость второго шарика после взаимодействия как V, запиши импульс P второго шарика после взаимодействия
Шаг 7. Обрати внимание, что в результате упругого столкновения шарики будут двигаться в разные стороны. Запиши суммарный импульс шариков после взаимодействия
Шаг 8. Поскольку два шарика являются замкнутой системой, то для них выполняется закон сохранения импульса: импульс системы до взаимодействия равен импульсу системы после взаимодействия. Составь уравнение согласно закону сохранения импульса и реши его относительно V с точностью до десятых
ответ: h = 0,8 м.
Объяснение:
Кинетическая энергия брусков после столкновения где v — скорость системы после удара, определяемая из закона сохранения импульса на горизонтальном участке: m1v1 = (m1 + m2)v.
Исключая из системы уравнений скорость v, получим:
Кинетическая энергия первого бруска перед столкновением определяется из закона сохранения механической энергии при скольжении по наклонной плоскости: что даёт выражение
Подставляя значения масс и энергии из условия, получим численное значение h = 0,8 м
h = 0,8 м.
На обеих рисунках рычаги в равновесии
Объяснение:
У нас два момента силы М1 и М2 (слева и справа от центра рычага)
M1 = F1 · L1
M2= F2 · L2
Ну и приравниваем их так как моменты всё же РАВНЫ M1=M2
F1 · L1 = F2 · L2
Если моменты силы равны тот рычаг будет в РАВНОВЕСИИ. Это нам надо и выяснить.
Предположим что каждая гиря - 1Дж, каждое деление на рычагу 1 см.
Подсчитываем что там на рисунке и подставляем в формулу
На первом рисунке (слева)
слева рычага: L1 = 4 см ; F1 = 1 Дж
M1 = F1 · L1
М1 = 4 * 1 ; М1 = 4
справа рычага: L = 2 см ; F = 2 Дж
M2 = F2 · L2
М2 = 2 *2 ; М2 = 4
Моменты ОДИНАКОВЫ, значит РАВНОВЕСИЕ
На втором рисунке (справа)
слева рычага: L1 = 2 см ; F1 = 3 Дж
M1 = F1 · L1
М1 = 2 * 3 ; М1 = 6
справа рычага: L = 3 см ; F = 2 Дж
M2 = F2 · L2
М2 = 3 *2 ; М2 = 6
Моменты ОДИНАКОВЫ, значит РАВНОВЕСИЕ
Давай немного теории:
Сила, с которой тело давит на опору , называют весом.
Вес тела обозначают P и измеряют в ньютонах ( H ) ( а если в килограммах то в 9,8 раз меньше m=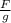
, это будет уже масса). Если у тебя 45 кг - это твоя масса, а весишь ты 450 Ньютон. То есть давишь на весы с силой 450 Ньютон.
Любую силу обозначают через F . Хотя в данном случае можно применить Р.
Произведение модуля силы, вращающей тело, на её плечо называется моментом силы.
Рычаг находится в равновесии под действием двух сил, если момент силы, вращающей его по часовой стрелке, равен моменту силы, вращающей его против часовой стрелки.
Это правило, называемое правилом моментов, можно записать в виде формулы: M1=M2 .
Момент силы M = F · L