Два тела массы которых 50 г и 100 г, лежат на горизонтальной поверхности стола на расстоянии 1 м. С какой силой они действуют друг на друга?
Задача 2.
Два одинаковых шарика, которые можно считать материальными точками, находятся на расстоянии 0,1 м друг от друга и притягиваются с силой 6,67 * 10-9 Н. Чему равна масса каждого шарика? (G = 6.67 *10-11 Н*м2/кг2)
1502 м
Объяснение:
Поскольку сопротивлением воздуха можно пренебречь, на тело действует только сила тяжести.
Рассмотрим вертикальный и горизонтальный полет отдельно.
Вертикальное движение мяча является равноускоренным с ускорением g.
Горизонтальное движение является равномерным.
Начальная вертикальная скорость:
Начальная горизонтальная скорость:
Полет заканчивается, когда мяч падает на землю.
Найдем время полета:
Получаем обычное квадратное уравнение. Решая его, при условии что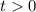
получаем
За это время горизонтально мяч пролетит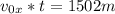
начальная деформация h
массы брусков m1, m2
скорость первого бруска в момент когда отпускают второй
m1 v1^2 / 2 = k h^2 / 2
v1 = h корень (k / m1)
ведём отсчёт времени и координат брусков от момента и положений, когда отпускают второй
d^2 x1 / dt^2 = - k/m1 (x1-x2), d^2 x2 / dt^2 = - k/m2 (x2-x1)
dx1 / dt = v1 при t = 0, dx2 / dt = 0 при t = 0
вычитая из первого второе получим
d^2 (x1-x2) / dt^2 = (-k/m1 - k/m2) (x1-x2)
откуда ясно, что величина (x1-x2) будет испытывать гармонические колебания с частотой омега = корень (k/m1 + k/m2)
в начальный момент d(x1-x2) / dt = v1, x1-x2 = 0
при нулевой координате скорость максимальна
амплитуда равна максимальная скорость делить на частоту
A = v1 / омега = h корень (k / m1) / корень (k/m1 + k/m2) =
= h корень (1/m1) / корень (1/m1 + 1/m2) = h корень (m2/(m1+m2))
амплитуда величины x1-x2 это и есть максимальная деформация пружины
10 * корень (16/25) = 8