Если решать эту задачу по школьному, без привлечения инструментария матанализа, то рассуждать можно следующим образом, - в любой точке траектории ускорение свободного падения может быть разложено на две составляющих - вдоль касательной к траектории (нормальное ускорение) и вдоль нормали к траектории (центростремительное ускорение), нам нужна вторая величина, так как она позволяет рассчитать искомый радиус. В наивысшей точке подъема мяча, очевидно, что центростремительное ускорение целиком совпадает с ускорением свободного падения:
Откуда:
Горизонтальная составляющая скорости будет везде одинакова и равна (учтем что 54 км/ч=15 м/с):
11,25 м
Объяснение:
Если решать эту задачу по школьному, без привлечения инструментария матанализа, то рассуждать можно следующим образом, - в любой точке траектории ускорение свободного падения может быть разложено на две составляющих - вдоль касательной к траектории (нормальное ускорение) и вдоль нормали к траектории (центростремительное ускорение), нам нужна вторая величина, так как она позволяет рассчитать искомый радиус. В наивысшей точке подъема мяча, очевидно, что центростремительное ускорение целиком совпадает с ускорением свободного падения:
Откуда:
Горизонтальная составляющая скорости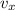
будет везде одинакова и равна (учтем что 54 км/ч=15 м/с):
Искомый радиус кривизны траектории:
Легкая задача.
Дано:
M=0,032кг/моль.
V=700м/с^2;
R=8,31 Дж/(моль*К).
T=?
Для начала, разберемся с формулой, нам известна формула средней квадратичной скорости молекулы. Формула имеет вид:
v2cp=(3*k*T)/m0
Формула (1).
Т.к. k=R/Na, а m0=M/Na. (Нам нужны эти преобразования, чтобы упростить формулу, и перейти к нашему условию).
Подставим эти формулы в (1)
v^2(cp)=(3*R*T/Na)*(Na/M);
Получаем:
v^2(cp)=3*R*T/M;
Все данные нам известны, подставляем данные:
v^2(cp)*M=3*R*T;
T=v^2(cp)*M/3*R;
T=490000*0,032/3*8,31=628,96=629К.
Либо, переводя в градусы, получаем:
T=629-273=356 градусов Цельсия.