1. Т. к масло залили до верху этого сосуда, но при этом масло менее плотная жидкость по сравнению с водой, то следовательно масло будет вытеснять более плотную жидкость, значит чтобы заполнить до верху сосуд маслом понадобится объем, равный:
2. Т. к сосуды одинаковы, значит однаковы их поперечные сечения, следовательно можно воспользоваться условием несжимаемости жидкости, это означает какой объем вытеснило масло, точно такой же объем будет в первом сосуде, и т. к сечения равны, значит равны высоты:
3. Далее можно записать равенство гидростатических давлений на одинаковых высотах:
Объём горячей и холодной воды равен 250 л., так как наполнена вся ванна.
Следовательно mх.+mг.=mo.=p*V
Где mx.-масса холодной воды,
mг.-масса горячей воды,
mo.-масса общая (масса смеси холодной и горячей воды)
p-плотность смеси горячей и холодной воды (равна плотности обычной воды и равна 1000 кг/м³)
V-оъём ванны (объём смеси горячей и холодной воды и равна 250 л.)
1) mx.+mг.=1000*(250/1000)
Объём в СИ измеряется в м³, а чтобы литры перевести в м³, надо литры делить на 1000, следовательно записываем не 250, а 250/1000
mх.+mг.=250 кг. => mх.=250-mг.
2) Составим уравнение теплового баланса:
Q1=Q2
° Q1=c*mх.*(tк.-tн.) где Q1-теплота полученная холодной водой, c-удельная теплоёмкость воды (она всегда равна 4200 Дж/(кг.*°C)), mх.-масса холодной воды, tк.-температура конечная (температура смеси и по условию задачи равна 40°C), tн.-температура начальная у холодной воды (по условию равна 10°C).
° Q2=c*mг.*(tн.-tк.) где Q2-теплота отданная горячей водой, c-удельная теплоёмкость воды (она всегда равна 4200 Дж/(кг.*°C)), mг.-масса горячей воды, tк.-температура конечная (температура смеси и по условию задачи равна 40°C), tн.-температура начальная у горячей воды (по условию равна 60°C).
Подставляем это всё в уравнение теплового баланса
Q1=Q2
c*mх.*(tк.-tн.)=c*mг.*(tн.-tк.)
Вместо mx. подставляем 250-mг., так как в 1-ом действии мы это доказали, что mх.=250-mг.
c*(250-mг.)*(40-10)=c*mг.*(60-40)
Вместо c можно поставить 4200 Дж/(кг.*°C), но в данном случае их можно сократить.
(250-mг.)*30=mг.*20
Расскрываем скобки
30*250-30*mг.=20*mг.
Переносим произведение -30*mг. в правую часть с противоположным знаком
30*250=20*mг.+30*mг.
30*250=50*mг.
mг.=5*30=150 кг.
Если в задаче имеется в виду какой объём горячей воды нужен, а не масса горячей воды, то:
Vг.=mг./p где Vг.-объём горячей воды, mг.-масса горячей воды (как мы вычислили она равна 150 кг.), p-плотность воды (она всегда равна 1000 кг/м³)
Vг.=150/1000=0,15 м³ или 0,15 м³ * 1000= 150 л. (литров).
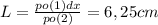
Объяснение:1. Т. к масло залили до верху этого сосуда, но при этом масло менее плотная жидкость по сравнению с водой, то следовательно масло будет вытеснять более плотную жидкость, значит чтобы заполнить до верху сосуд маслом понадобится объем, равный:
2. Т. к сосуды одинаковы, значит однаковы их поперечные сечения, следовательно можно воспользоваться условием несжимаемости жидкости, это означает какой объем вытеснило масло, точно такой же объем будет в первом сосуде, и т. к сечения равны, значит равны высоты:
3. Далее можно записать равенство гидростатических давлений на одинаковых высотах:
Объём горячей и холодной воды равен 250 л., так как наполнена вся ванна.
Следовательно mх.+mг.=mo.=p*V
Где mx.-масса холодной воды,
mг.-масса горячей воды,
mo.-масса общая (масса смеси холодной и горячей воды)
p-плотность смеси горячей и холодной воды (равна плотности обычной воды и равна 1000 кг/м³)
V-оъём ванны (объём смеси горячей и холодной воды и равна 250 л.)
1) mx.+mг.=1000*(250/1000)
Объём в СИ измеряется в м³, а чтобы литры перевести в м³, надо литры делить на 1000, следовательно записываем не 250, а 250/1000
mх.+mг.=250 кг. => mх.=250-mг.
2) Составим уравнение теплового баланса:
Q1=Q2
° Q1=c*mх.*(tк.-tн.) где Q1-теплота полученная холодной водой, c-удельная теплоёмкость воды (она всегда равна 4200 Дж/(кг.*°C)), mх.-масса холодной воды, tк.-температура конечная (температура смеси и по условию задачи равна 40°C), tн.-температура начальная у холодной воды (по условию равна 10°C).
° Q2=c*mг.*(tн.-tк.) где Q2-теплота отданная горячей водой, c-удельная теплоёмкость воды (она всегда равна 4200 Дж/(кг.*°C)), mг.-масса горячей воды, tк.-температура конечная (температура смеси и по условию задачи равна 40°C), tн.-температура начальная у горячей воды (по условию равна 60°C).
Подставляем это всё в уравнение теплового баланса
Q1=Q2
c*mх.*(tк.-tн.)=c*mг.*(tн.-tк.)
Вместо mx. подставляем 250-mг., так как в 1-ом действии мы это доказали, что mх.=250-mг.
c*(250-mг.)*(40-10)=c*mг.*(60-40)
Вместо c можно поставить 4200 Дж/(кг.*°C), но в данном случае их можно сократить.
(250-mг.)*30=mг.*20
Расскрываем скобки
30*250-30*mг.=20*mг.
Переносим произведение -30*mг. в правую часть с противоположным знаком
30*250=20*mг.+30*mг.
30*250=50*mг.
mг.=5*30=150 кг.
Если в задаче имеется в виду какой объём горячей воды нужен, а не масса горячей воды, то:
Vг.=mг./p где Vг.-объём горячей воды, mг.-масса горячей воды (как мы вычислили она равна 150 кг.), p-плотность воды (она всегда равна 1000 кг/м³)
Vг.=150/1000=0,15 м³ или 0,15 м³ * 1000= 150 л. (литров).
ответ: необходимо 150 л. горячей воды.