Запишем уравнение гармонических колебаний в общем виде:
Будим считать, что маятник, в начальный момент времени, находился в положении максимального смещения от положения равновесия. В этом случае, когда мы отпустим маятник, он начнет совершать гармонические, незатухающие колебания.
Отсюда ⇒ (1)
Мы знаем, что потенциальную энергию пружинного маятника W, в любой момент времени t, можно вычислить как kx²(t)/2, а кинетическую энергию E, как mv²(t)/2.
То-есть , но согласно уравнению (1) получим
Аналогично , однако мы знаем, что
Тогда ⇒ , а это значит что
Поэтому , так как , то ⇒ (2)
Теперь определим cos²(ωt), мы знаем, что в нашем случае, в момент момент времени t растяжение пружины маятника составило А/3, тогда согласно уравнению (1) ⇒ , следовательно
ответ: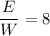
Объяснение:
Запишем уравнение гармонических колебаний в общем виде:
Будим считать, что маятник, в начальный момент времени, находился в положении максимального смещения от положения равновесия. В этом случае, когда мы отпустим маятник, он начнет совершать гармонические, незатухающие колебания.
Отсюда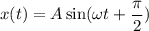 ⇒
⇒ 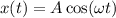 (1)
(1)
Мы знаем, что потенциальную энергию пружинного маятника W, в любой момент времени t, можно вычислить как kx²(t)/2, а кинетическую энергию E, как mv²(t)/2.
То-есть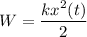 , но согласно уравнению (1) получим
, но согласно уравнению (1) получим 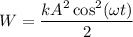
Аналогично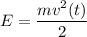 , однако мы знаем, что
, однако мы знаем, что 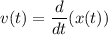
Тогда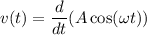 ⇒
⇒ 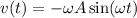 , а это значит что
, а это значит что 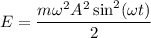
Поэтому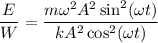 , так как
, так как 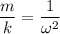 , то
, то 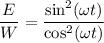 ⇒
⇒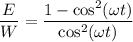 (2)
(2)
Теперь определим cos²(ωt), мы знаем, что в нашем случае, в момент момент времени t растяжение пружины маятника составило А/3, тогда согласно уравнению (1)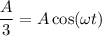 ⇒
⇒ 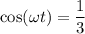 , следовательно
, следовательно 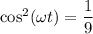
Возвращаясь к уравнению (2) получим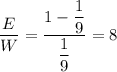
1(Абс.Упр.Центр.)
(для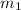 , двигавшегося сначала с пололжительной скоростью),
, двигавшегося сначала с пололжительной скоростью),
(для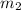 , двигавшегося сначала с отрицательной скоростью).
, двигавшегося сначала с отрицательной скоростью).
оба тела разворачиваются.
1(Абс.Неупр.)
2.33 м/с ;
2) 2.5 см .
Объяснение:
1(Абс.Упр.)
Случай абсолютно упругого центрального удара (взаимодействие по линии центров масс, параллельной направлению движения):
где: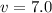 м/с и
м/с и 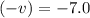 м/с – начальные скорости тел
м/с – начальные скорости тел 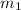 и
и 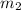 , а
, а 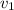 и
и 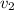 – конечные скорости тел
– конечные скорости тел 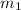 и
и 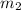 .
.
Разделим оба уравнения на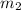 , а второе ещё и удвоим:
, а второе ещё и удвоим:
Сделаем перестановки:
(*)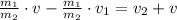 , из Закона Сохранения Импульса;
, из Закона Сохранения Импульса;
Разделим второе уравнение на первое, учтя, что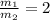 :
:
Оба тела развернутся и будут иметь скорости:
1(Абс.Неупр.)
Случай абсолютно неупругого удара:
2)
В положении равновесия:
Из теории колебаний известно, что:
Тогда: