ответ: 8 ч
Объяснение:
Введем неизвестные переменные:
S - расстояние между пристанями
V₁ - скорость лодки
V₂ - скорость реки
S = Vt
(1) S = t₁(V₁ + V₂)
(2) S = t₂(V₁ + V₂)
(3) t₁(V₁ + V₂) = t₂(V₁ + V₂) - приравниваем
(4) t₁V₁ + t₁V₂ = t₂V₁ - t₂V₂ - раскрываем скобки
(5) t₁V₂ + t₂V₂ = t₂V₁ - t₁V₁ - скор реки и лодки по разные стороны
(6) V₂(t₁ + t₂) = V₁(t₂ - t₁) - выносим общий множитель
(7) V₁ = - выражаем скор лодки
(8) t₃ = - искомое время
(9) t₃ = - подставляем (1)
(10) t₃ = + = + t₁ - раскрываем скобки и сокращаем
(11) t₃ = + t₁ - подставляем (7) вместо V₁
(12) t₃ = + t₁ - конечная частная формула (в ней только известные)
(13) t₃ = + 2 = + 2 = 8 ч
В ;
А ;
Вт ;
Вт.
Токи через , и равны, как неразветвляющиеся: А ;
Мощности на , и равны, соответственно:
Вт Вт ;
Напряжения на , и равны, соответственно:
В В ;
Общее напряжение на и участке, состоящем из , и равны, как параллельно подключённые:
В
Мощность на равна:
Ток через по закону Ома:
А А ;
Токи через и , как, соответственно, разветвляющийся и стекающийся, находятся суммированием токов через и через участок, состоящий из , и :
Мощности на и равны, соответственно:
Вт
Напряжения на и равны, соответственно:
Общее напряжение на и участке, состоящем из , и (с распараллеливанием) равны, как параллельно подключённые:
Общий ток, как разветвляющийся:
А А А ;
Общая мощность:
Вт Вт Вт ;
Баланс мощности:
;
.
ответ: 8 ч
Объяснение:
Дано: t₁ = 2 ч - по течению; t₂ = 3 ч - против течения; t₃ = ? - по течению с выкл моторомВведем неизвестные переменные:
S - расстояние между пристанями
V₁ - скорость лодки
V₂ - скорость реки
S = Vt
(1) S = t₁(V₁ + V₂)
(2) S = t₂(V₁ + V₂)
(3) t₁(V₁ + V₂) = t₂(V₁ + V₂) - приравниваем
(4) t₁V₁ + t₁V₂ = t₂V₁ - t₂V₂ - раскрываем скобки
(5) t₁V₂ + t₂V₂ = t₂V₁ - t₁V₁ - скор реки и лодки по разные стороны
(6) V₂(t₁ + t₂) = V₁(t₂ - t₁) - выносим общий множитель
(7) V₁ =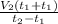 - выражаем скор лодки
- выражаем скор лодки
(8) t₃ =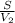 - искомое время
- искомое время
(9) t₃ =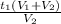 - подставляем (1)
- подставляем (1)
(10) t₃ =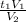 +
+ 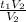 =
= 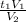 + t₁ - раскрываем скобки и сокращаем
+ t₁ - раскрываем скобки и сокращаем
(11) t₃ =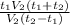 + t₁ - подставляем (7) вместо V₁
+ t₁ - подставляем (7) вместо V₁
(12) t₃ =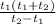 + t₁ - конечная частная формула (в ней только известные)
+ t₁ - конечная частная формула (в ней только известные)
(13) t₃ =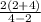 + 2 =
+ 2 = 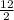 + 2 = 8 ч
+ 2 = 8 ч
Объяснение:
Токи через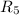 ,
, 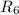 и
и 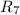 равны, как неразветвляющиеся:
равны, как неразветвляющиеся: 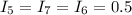 А ;
А ;
Мощности на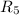 ,
, 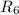 и
и 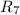 равны, соответственно:
равны, соответственно:
Напряжения на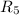 ,
, 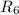 и
и 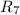 равны, соответственно:
равны, соответственно:
Общее напряжение на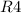 и участке, состоящем из
и участке, состоящем из 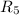 ,
, 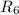 и
и 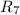 равны, как параллельно подключённые:
равны, как параллельно подключённые:
Мощность на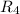 равна:
равна:
Ток через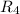 по закону Ома:
по закону Ома:
Токи через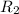 и
и 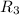 , как, соответственно, разветвляющийся и стекающийся, находятся суммированием токов через
, как, соответственно, разветвляющийся и стекающийся, находятся суммированием токов через 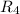 и через участок, состоящий из
и через участок, состоящий из 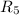 ,
, 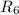 и
и 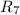 :
:
Мощности на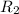 и
и 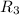 равны, соответственно:
равны, соответственно:
Напряжения на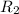 и
и 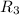 равны, соответственно:
равны, соответственно:
Общее напряжение на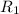 и участке, состоящем из
и участке, состоящем из 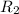 ,
, 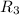 и
и 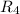 (с распараллеливанием) равны, как параллельно подключённые:
(с распараллеливанием) равны, как параллельно подключённые:
Мощность на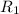 равна:
равна:
Ток через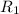 по закону Ома:
по закону Ома:
Общий ток, как разветвляющийся:
Общая мощность:
Баланс мощности: