Гирька весом р=4,9 н, привязанная к резиновому шнуру длиной l0 описывает в горизонтальной плоскости окружность. скорость вращения гирьки соответствует частоте υ=2 об/с. угол откло нения резинового шнура от вертикали равен β=30°. найти длину l0 нерастянутого резинового шнура. для растяжения шнура на x1=1 см требуется сила f1=6,0 н.

Объяснение:

Решение

Рисунок прилагается.

Второй закон Ньютона запишем в виде

F(вектор)=m*a(вектор)

где равнодействующая сила  

F(вектор)

 F(вектор)= m*g(вектор)+T(вектор)

Спроецируем на выбранные оси координат

Y:

T*cos(alpha)-mg=0

T*cos(alpha)=mg

T=mg/cos(alpha)

По условию Гирька весит Р=4,9 Н.

Так как вдоль оси ОУ ускорения равно 0, то по определению Р=m*g

Подставим

T=P/cos(alpha)=4.9/cos30=4.9/0.87=5.66 Н

Эта найденная сила и приводит к тому, что длина шнура меняется.

А величина этого изменения зависит от коэффициента упругости (жесткости) шнура, по закону

T=k*Δl

Отсюда Δl=T/k

k нам не дано, но известно из условий, что Для растяжения шнура на x1=1 см требуется сила F1=6,0 Н. Другими словами F=k*Δx; k=F/Δx=6/0,01=600

Теперь мы знаем k и подставим его

Δl=T/k=5,66/600=0,0094 м

Длина растянутого шнура это l=l0+Δl

Отсюда

l0=l-Δl

l неизвестна. Найдем эту длину.

Заметим что по подобию двух треугольников

Отсюда l=R*T/F

Так как F действует вдоль ОХ, то нам нужны проекции сил на эту ось

F=T*Sin(alpha)=m*a(центростремительное)

a(центростремительное)=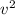/R

F=T*Sin(alpha)=m*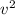/R

Линейная скорость v = w*R

F=T*Sin(alpha)=m*

w=2*п*n

F=T*Sin(alpha)=m*

Подставим F в формулу ниже

l=R*T/F=R*T/=T/4*m*,

где m=Р/g

l=T*g/4*P* =0.0716 м

l0=l-Δl=0.0716-0,0094=0,0624 м

l0 нерастянутого резинового шнура = 0,0624 м = 62,4 мм

l растянутого резинового шнура = 0.0716 м = 71,6 мм