Груз массой 25 кг перемещается по наклонной плоскости под действием силы тяги 400 Н, направленной под углом 30° к плоскости. Коэффициент трения груза о плоскость 0,1. Угол наклона плоскости к горизонте составляет 15°. Определите ускорение груза.
Уравнение теплового баланса говорит, что какое количество теплоты отвели от горячей воды, такое же количество теплоты подвели к холодной воде (логично, нет же потерь энергии на нагревание всего отсального): Qх = -Qг Знак "минус" говорит о том, что раз от горячей воды теплота уходит, то величина Qг < 0. Со знаком "минус" она станет положительной, как и Qх.
cх*mх*Δtх = -cг*mг*Δtг, где cх и cг – удельная теплоёмкость холодной и горячей воды соответственно, Дж/(кг*°С); mх и mг – масса холодной и горячей воды соответственно, кг; Δtх и Δtг – изменение температуры холодной и горячей воды соответственно, °С.
Считаем, что удельная теплоёмкость воды не зависит от её температуры: cх = cг = c = 4200 Дж/(кг*°С).
Начальная температура холодной воды tх = 20 °С, начальная температура горячей воды tг = 90 °С, установившаяся температура воды t = 50 °С, тогда: Δtх = t - tх Δtг = t - tг
№1. а) сила Архимеда одинакова (она определяется объемом погруженного в жидкость тела); б) так как плотность меди больше плотности алюминия, объем медного шара равной массы будет меньше, соответственно сила Архимеда, действующая на него будет меньше.
№2. С гидростатического взвешивания измеряют плотности твердых тел и жидкостей. В первом случае твердое тело взвешивают в воздухе и в жидкости, определяя массу и объем, соответственно, а потом деля одно на другое. Во втором - берут тело известной массы и объема, взвешивают его в жидкости, определяя силу Архимеда, а затем плотность жидкости.
№3. Если взять плотность гранита 2600 кг/м^3, то объем камня равен 0.0038 м^3, а сила Архимеда, действующая на него = 38 Н ( = 1000 кг/м^3 - плотность воды). Вычитая из силы тяжести (mg=10 кг*9.8 м/с^2 = 98 Н) силу Архимеда получим силу, которую надо приложить, чтобы поднять камень, 60 Н.
Qх = -Qг
Знак "минус" говорит о том, что раз от горячей воды теплота уходит, то величина Qг < 0. Со знаком "минус" она станет положительной, как и Qх.
cх*mх*Δtх = -cг*mг*Δtг, где
cх и cг – удельная теплоёмкость холодной и горячей воды соответственно, Дж/(кг*°С);
mх и mг – масса холодной и горячей воды соответственно, кг;
Δtх и Δtг – изменение температуры холодной и горячей воды соответственно, °С.
Считаем, что удельная теплоёмкость воды не зависит от её температуры:
cх = cг = c = 4200 Дж/(кг*°С).
Начальная температура холодной воды tх = 20 °С, начальная температура горячей воды tг = 90 °С, установившаяся температура воды t = 50 °С, тогда:
Δtх = t - tх
Δtг = t - tг
Тогда:
c*mх*(t - tх) = -c*mг*(t - tг)
c*mх*(t - tх) = c*mг*(tг - t)
mх*(t - tх) = mг*(tг - t)
mг = mх*(t - tх) / (tг - t)
mг = 3 кг * (50 °С - 20 °С) / (90 °С - 50 °С)
mг = 2,25 кг
№1. а) сила Архимеда одинакова (она определяется объемом погруженного в жидкость тела); б) так как плотность меди больше плотности алюминия, объем медного шара равной массы будет меньше, соответственно сила Архимеда, действующая на него будет меньше.
№2. С гидростатического взвешивания измеряют плотности твердых тел и жидкостей. В первом случае твердое тело взвешивают в воздухе и в жидкости, определяя массу и объем, соответственно, а потом деля одно на другое. Во втором - берут тело известной массы и объема, взвешивают его в жидкости, определяя силу Архимеда, а затем плотность жидкости.
№3. Если взять плотность гранита 2600 кг/м^3, то объем камня равен 0.0038 м^3, а сила Архимеда, действующая на него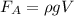 = 38 Н (
= 38 Н (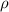 = 1000 кг/м^3 - плотность воды). Вычитая из силы тяжести (mg=10 кг*9.8 м/с^2 = 98 Н) силу Архимеда получим силу, которую надо приложить, чтобы поднять камень, 60 Н.
= 1000 кг/м^3 - плотность воды). Вычитая из силы тяжести (mg=10 кг*9.8 м/с^2 = 98 Н) силу Архимеда получим силу, которую надо приложить, чтобы поднять камень, 60 Н.