Груз массой 40 кг касается вертикально стоящей пружины на асфальте с коэффициентом жесткости 50 н/м, не деформируя её. через какое время он достигнет максимальной скорости при предоставлении ему свободы? при деформации пружина вертикальна. g=10 м/с кв.

Показать ответ

Ответ:

ДЕСПАСИТТО58

05.10.2020 02:15

Численное значение ускорения свободного падения не играет никакой роли. И на Луне и на Марсе время достижения максимальной скорости было бы одинаковым. Отличалась бы только сама эта максимальная скорость. Поскольку, как хорошо известно, частота пружинных колебаний в продольном однородном потенциальном поле происходят с той же частотой, что и в его отсутствии. Каждую четверть периода гармонических колебаний – модуль скорости меняет своё значение от нулевого до амплитудного и наоборот.

БЕЗ ДОКАЗАТЕЛЬСТВА ФАКТА НЕИЗМЕННОМТИ ПЕРИОДА КОЛЕБАНИЙ:

$t = \frac{T}{4} = \frac{1}{4} \cdot 2 \pi \sqrt{ \frac{m}{k} } = \frac{\pi}{2} \sqrt{ \frac{m}{k} } \ ;$

$t = \frac{\pi}{2} \sqrt{ \frac{m}{k} } \approx \frac{\pi}{2} \sqrt{ \frac{40}{50} } \approx 1.4$ сек ;

ВТОРОЙ с доказательством неизменности периода:

Будем для начала откладывать координату вниз от начального положения груза. На груз всё время будет действовать сила:

$F = mg - kx = - ( kx - mg ) = - k ( x - \frac{mg}{k} ) \ ;$

Теперь станем откладывать координату от точки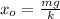 $x_o = \frac{mg}{k}$ и получим смещённую координату:

$x_c = x - x_o \ ;$ и теперь уже можем записать уравнение для силы так:

$F = - k ( x - x_o ) = - k x_c \ ;$

$ma = - k x_c \ ;$

$mx'' = mx_c'' = - k x_c \ ;$

Последнее – это уравнение гармонических колебаний с циклической частотой:

$\omega = \sqrt{ \frac{k}{m} } \ ,$ и периодом:

$T = \frac{ 2 \pi }{ \omega } = 2 \pi \sqrt{ \frac{k}{m} } \ ,$ нас интересует четверть-период, так что:

$t = \frac{T}{4} = \frac{\pi}{2} \sqrt{ \frac{m}{k} } \approx \frac{\pi}{2} \sqrt{ \frac{40}{50} } \approx 1.4$ сек ;

ТРЕТИЙ с доказательством неизменности периода:

На груз всё время будет действовать сила:

$F = mg - kx = - ( kx - mg ) = - k ( x - \frac{mg}{k} ) \ ;$

$ma = - k ( x - \frac{mg}{k} ) \ ;$

$mx'' = - k ( x - \frac{mg}{k} ) \ ;$

$m( x - \frac{mg}{k} )'' = - k ( x - \frac{mg}{k} ) \ ;$

Это уравнение гармонических колебаний с циклической частотой:

$\omega = \sqrt{ \frac{k}{m} } \ ,$ и периодом:

$T = \frac{ 2 \pi }{ \omega } = 2 \pi \sqrt{ \frac{k}{m} } \ ,$ нас интересует четверть-период, так что:

$t = \frac{T}{4} = \frac{\pi}{2} \sqrt{ \frac{m}{k} } \approx \frac{\pi}{2} \sqrt{ \frac{40}{50} } \approx 1.4$ сек ;

ЧЕТВЁРТЫЙ с доказательством неизменности периода:

Будем откладывать координату вниз от начального положения груза. По закону сохранения энергии:

$- mgx + \frac{kx^2}{2} + \frac{mv^2}{2} = const \ ;$

Возьмём производную от обеих частей уравнения:

$- mgx' + kxx' + mvv' = 0 \ ;$

$mgv - kxv = mvx'' \ ;$

$mg - kx = mx'' \ ;$

$- k ( x - \frac{mg}{k} ) = mx'' \ ;$

$( x - \frac{mg}{k} )'' = - \frac{k}{m} ( x - \frac{mg}{k} ) \ ;$

Это уравнение гармонических колебаний с циклической частотой:

$\omega = \sqrt{ \frac{k}{m} } \ ,$ и периодом:

$T = \frac{ 2 \pi }{ \omega } = 2 \pi \sqrt{ \frac{k}{m} } \ ,$ нас интересует четверть-период, так что:

$t = \frac{T}{4} = \frac{\pi}{2} \sqrt{ \frac{m}{k} } \approx \frac{\pi}{2} \sqrt{ \frac{40}{50} } \approx 1.4$ сек .

0,0(0 оценок)

Популярные вопросы: Физика

nataliinfp0co9o

22.07.2020 20:22

Здравствуйте Движение проводника с током в магнитном поле,какой силой действует магнитное поле на проводник?...

DAYDEMON

06.04.2023 03:44

При якому струмі проходив електроліз cuso4 якщо на катоді виділилося 33 мг міді протягом 100 с...

aurantiuma

17.03.2021 17:32

1.Какой массы груз можно поднять равномерно вверх на высоту 12 м, если совершаемая при этом работа равна 18 кДж2.Найти мощность двигателя, если он за 5 минут совершает работу...

AlinaTishka

16.05.2021 14:55

Термодинамика. При изохорическом охлаждении 1 моля идеального газа во внешнюю среду отдано 15 Дж теплоты. Определить разность между величинами внутренней энергии газа в конце...

полина2054

22.03.2020 14:46

Чому дорівнює фокусна відстань лінзи, якщо її оптична сила становить (-5,0 дптр). Яка це лінза збиральна чи розсіювальна?...

Yarik200825

03.11.2022 04:04

Установите соответствие между физическими понятиями и иллюстрирующими их примерами. Для каждого физического понятия из первого столбца подберите пример из второго столбца.ФИЗИЧЕСКИЕ...

Oleg2156

01.07.2022 09:21

Нерасияжимая невесомая нить AB приводит в движение стержень OA, шарнирно укреплённый в точке A, зная скорость точки B, направленный как показано на рисунке и равный v. Угол,...

anyutatelichuk

28.09.2021 19:00

предмет расположен на расстоянии 15 см от линзы а изображение предмета на экране находится перед линзой на расстоянии 5 см вычислите фокусное расстояние этой линзы...

саня45рг

21.02.2021 11:39

За 10 с сила струму в провіднику опором 25 Ом рівномірно зростає від нуля до деякого максимального значення. За цей час у ньому виділилася кількість теплоти 40 кДж. Визначити...

begemot20031

26.01.2023 01:14

Лампа розжарення з вольфрамовою ниткою потужністю Р = 200 Вт розрахована на напругу U = 220 В. Робоча температура нитки розжарювання Т = 2700 К. Діаметр нитки d = 0,03 мм....

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку