Согласно II закону Ньютона ma=mg_{1}[/tex], где - ускорение свободного падения на той высоте, где летит спутник.
Спутник двигается по окружности под действием только силы тяжести, поэтому
, где - радиус орбиты, по которой движется спутник.
Откуда
С другой стороны, сила тяжести - это сила всемирного тяготения, поэтому справедливо следующее: , где M - масса планеты, G - гравитационная постоянная.
Отсюда
Теперь запишем то же самое для поверхности планеты: , g - ускорение свободного падения у поверхности планеты (заданное в условии), R - радиус планеты.
Подставим в последнее уравнение массу планеты М и получим:
И отсюда находим R:
R=3 400 000 м=3 400 км
Согласно II закону Ньютона ma=mg_{1}[/tex], где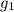 - ускорение свободного падения на той высоте, где летит спутник.
- ускорение свободного падения на той высоте, где летит спутник.
Спутник двигается по окружности под действием только силы тяжести, поэтому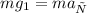
Откуда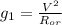
С другой стороны, сила тяжести - это сила всемирного тяготения, поэтому справедливо следующее: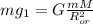 , где M - масса планеты, G - гравитационная постоянная.
, где M - масса планеты, G - гравитационная постоянная.
Отсюда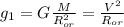
Отсюда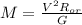
Теперь запишем то же самое для поверхности планеты: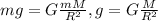 , g - ускорение свободного падения у поверхности планеты (заданное в условии), R - радиус планеты.
, g - ускорение свободного падения у поверхности планеты (заданное в условии), R - радиус планеты.
Подставим в последнее уравнение массу планеты М и получим: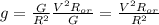
И отсюда находим R: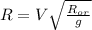
R=3 400 000 м=3 400 км