Используя схему электрической цепи, изображённый на рисунке 17, определите общее напряжение, если ампер метр показывает 5 а, r1=2 ом, r2=3 ом, r3=6 ом, r4=5 ом
Втавить пропускиВы уже знакомы со многими физическими величинами, которые применяются в • • • • • • • • (динамике) . Это, например, мера гравитационных и инертных свойств тела – • • • • • (масса) , мера действия одного тела на другое в отношении возникновения ускорения – • • • •(сила) , мера действия одного тела на другое в отношении совершаемого перемещения – • • • • • • (?) . Динамика – это • • • • • •(раздел) физики, изучающий причины движения тел, ставящий целью предсказать • • • • • • • •(характер) движения, если известны действующие на тело силы и его начальные • • • • • • •(значения) : координаты и • • • • • •(величину ?) скорости. Поскольку движение тел выглядит по-разному с точек зрения различных • • • • • • • • • • • • (систем отсчета) , необходимо выбрать такую • • • • • • •(систему) отсчёта, в которой законы динамики будут верны. Развитие физики показало, что • • • • • • • • • •(существуют) так называемые
• • • • • • • • • • • •(инерциональные) системы отсчёта, в которых любое тело, на которое не действуют другие тела, будет вечно • • • • • • • • •(сохранять) свою скорость. Это утверждение называется • • • • • •(первым) законом Ньютона и означает, что при • • • • • • • • • • (уравновешивании, компесации) сил движение тела будет зависеть только от его начальных условий – координат и вектора • • • • • • • •(скорости) . Инерциальные системы отсчёта лишь • • • • • • • •(справедливы ) при рассмотрении свободных тел, а далее • • • • • • • • • • • (?) для любых тел. Именно в инерциальных СО будут справедливы основные • • • • • •(законы) динамики.
Пусть масса акробата — m1, скорость акробата — v1, масса и скорость лошади — m2 и v2 соответственно. p1 — импульс акробата до вскакивания на лошадь, p1’ — после, p2 и р2’ — импульс лошади до и после вскакивания на неё акробата соответственно.
По закону сохранения импульса:
р1 + р2 = р1’ + р2’
Так как акробат вскочил на лошадь, импульс у них после вскакивания будет общим (назовём его р’):
р1 + р2 = р’
Импульс рассчитывается по формуле р = m*v, где m — масса, v — скорость. Тогда закон сохранения импульса для данной задачи можно записать как
m1v1 + m2v2 = v’(m1 + m2)
Здесь v’ — искомая скорость акробата на лошади;
p’ = v’(m1 + m2): массы складываются, так как акробата и лошадь теперь можно рассматривать как одно «тело», скорость которого мы ищем (мы ищем скорость лошади после прыжка акробата, а значит, скорость лошади, на которой сидит акробат).
физическими
величинами, которые
применяются в
• • • • • • • • (динамике)
. Это, например, мера гравитационных и
инертных свойств тела –
• • • • • (масса)
, мера действия одного тела на другое
в отношении возникновения ускорения –
• • • •(сила)
, мера действия одного
тела на другое в отношении совершаемого перемещения –
• • • • • • (?)
.
Динамика – это
• • • • • •(раздел)
физики, изучающий причины движения тел,
ставящий целью предсказать
• • • • • • • •(характер)
движения, если известны
действующие на тело силы и его начальные
• • • • • • •(значения)
: координаты
и
• • • • • •(величину ?)
скорости. Поскольку движение тел выглядит по-разному
с точек зрения различных
• • • • • • • • • • • • (систем отсчета)
, необходимо выбрать
такую
• • • • • • •(систему)
отсчёта, в которой законы динамики будут верны.
Развитие физики показало, что
• • • • • • • • • •(существуют)
так называемые
• • • • • • • • • • • •(инерциональные)
системы отсчёта, в которых любое тело, на которое
не действуют другие тела, будет вечно
• • • • • • • • •(сохранять)
свою скорость.
Это утверждение называется
• • • • • •(первым)
законом Ньютона и означает,
что при
• • • • • • • • • • (уравновешивании, компесации)
сил движение тела будет зависеть только
от его начальных условий – координат и вектора
• • • • • • • •(скорости)
.
Инерциальные системы отсчёта лишь
• • • • • • • •(справедливы )
при рассмотрении
свободных тел, а далее
• • • • • • • • • • • (?)
для любых тел. Именно в
инерциальных СО будут справедливы основные
• • • • • •(законы)
динамики.
ответ: 3,1 м/с
Объяснение:
Пусть масса акробата — m1, скорость акробата — v1, масса и скорость лошади — m2 и v2 соответственно. p1 — импульс акробата до вскакивания на лошадь, p1’ — после, p2 и р2’ — импульс лошади до и после вскакивания на неё акробата соответственно.
По закону сохранения импульса:
р1 + р2 = р1’ + р2’
Так как акробат вскочил на лошадь, импульс у них после вскакивания будет общим (назовём его р’):
р1 + р2 = р’
Импульс рассчитывается по формуле р = m*v, где m — масса, v — скорость. Тогда закон сохранения импульса для данной задачи можно записать как
m1v1 + m2v2 = v’(m1 + m2)
Здесь v’ — искомая скорость акробата на лошади;
p’ = v’(m1 + m2): массы складываются, так как акробата и лошадь теперь можно рассматривать как одно «тело», скорость которого мы ищем (мы ищем скорость лошади после прыжка акробата, а значит, скорость лошади, на которой сидит акробат).
Итак, m1v1 + m2v2 = v’(m1 + m2). Выразим отсюда v’ :
v’ =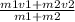
Подставим значения из условия:
v’ =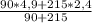
≈ 3,1 м/с