Из миномета ведут стрельбу по объектам, расположенным на склоне горы. на каком расстоянии от миномета будут падать мины, если их начальная скорость v, угол наклона горы α и угол стрельбы по отношению к горизонту β?

Показать ответ

Ответ:

853692

07.10.2020 16:12

ответ: $L=\dfrac{2v_{0}^{2} \sin(\beta -\alpha )}{g \cos\alpha }\left(\cos(\beta -\alpha )- tg\alpha\sin(\beta -\alpha)} \right)$

Объяснение:

Несколько уточним условие: миномет находиться у подножия горы.

Выбираем систему координат как показано на рисунке. При перемещении тела(мины) выпущенного из миномета, оно будет участвовать как в движении вдоль оси Ox, так и вдоль оси Oy.

При этом, такое движение в данной системе отсчета, можно описать следующим образом.

$Ox: x=v_{0} \cos(\beta -\alpha )t-\dfrac{g \sin\alpha t^{2} }{2} \\Oy: y=v_{0} \sin(\beta -\alpha )t-\dfrac{g \cos\alpha t^{2} }{2}$

Где t - время движения тела.

Рассмотрим более подробно движение вдоль оси Oy, определим в какие моменты времени $\tau$ координата, вдоль этой оси, будет равна 0.

$0=v_{0} \sin(\beta -\alpha ) \tau -\dfrac{g \cos\alpha \tau^{2} }{2}$ ⇒ $\tau \left( v_{0} \sin(\beta -\alpha )-\dfrac{g \cos\alpha \tau}{2}\right)=0$

Отсюда получим $\tau=0$ (в начальный момент времени) или $\tau=\dfrac{2v_{0} \sin(\beta -\alpha )}{g \cos\alpha }$ (1)(в конечный момент времени)

$\tau=0$ нас мало интересует, поэтому в дальнейшем будем рассматривать только второй корень $\tau=\dfrac{2v_{0} \sin(\beta -\alpha )}{g \cos\alpha }$ , по этого времени координата тела вдоль оси Ox станет максимальной, то есть эта координата и будет расстоянием от миномета, до того места, на котором будут падать мины. Соответственно, так как $Ox:x=v_{0} \cos(\beta -\alpha )t-\dfrac{g \sin\alpha t^{2} }{2}$ , то $L=v_{0} \cos(\beta -\alpha )\tau-\dfrac{g \sin\alpha \tau^{2} }{2}$ . Согласно уравнению (1) получим $L=v_{0} \cos(\beta -\alpha )\dfrac{2v_{0} \sin(\beta -\alpha )}{g \cos\alpha }-\dfrac{g \sin\alpha }{2}\left(\dfrac{2v_{0} \sin(\beta -\alpha )}{g \cos\alpha }\right)^{2}$ ⇒ $L= \dfrac{2v_{0}^{2} \sin(\beta -\alpha )\cos(\beta -\alpha )}{g \cos\alpha }-\dfrac{2v_{0}^{2} \sin\alpha \sin^{2} (\beta -\alpha)}{g \cos^{2}\alpha }}$ ⇒ $L=\dfrac{2v_{0}^{2} \sin(\beta -\alpha )}{g \cos\alpha }\left(\cos(\beta -\alpha )- \dfrac{\sin\alpha \sin(\beta -\alpha)}{\cos\alpha} \right)$ ⇒ $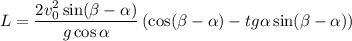L=\dfrac{2v_{0}^{2} \sin(\beta -\alpha )}{g \cos\alpha }\left(\cos(\beta -\alpha )- tg\alpha\sin(\beta -\alpha)} \right)$