ЛЮБЫЕ тела получают тепло, если их температура меньше, чем у окружающей среды. Холодная вода тоже может отдавать тепло, если воздух вокруг имеет меньшую температуру или в ней плавает лед, а температура воды больше нуля хоть немного.
Это продолжается, пока не наступит тепловой баланс (пока температуры тел не сравняются).
Вы зимой проветрили комнату, в ней воздух с температурой <0.
Но проходит немного времени и в комнате опять тепло, т.к. стены, мебель и другие вещи в комнате отдали свое тепло холодному воздуху и теперь у всех тел одинаковая температура.
Мясо из морозилки размораживают в холодной воде, а то оно при варке будет жестким. Холодные напитки делают еще более холодными, бросив в них кубики льда. Мама учит не пить напитки сразу из холодильника, пусть постоят, согреются))
Вывод: холодная вода может получать тепло (из холодильника ее вынули и она стоит в теплой комнате), но та же самая вода будет отдавать тепло, если в нее бросить лед или подлить еще более холодную воду. Все зависит от температуры тела, с которым эта вода соприкасается.
Чтобы рассчитать подобную схему, ее нужно преобразовать.
Резисторы R2, R3 и R5 соединены треугольником. Преобразуем это соединение в эквивалентную звезду. Ввиду того, что все три резистора имеют одинаковые номиналы, сделать это нетрудно:
R2y = R3y = R5y = R/3 (см. вложения 1, 2).
Теперь резисторы R1 и R2y соединены последовательно, а их эквивалентное сопротивление составляет
R12y = R1+R2y = R+R/3 = 4R/3.
Аналогично для R4 и R3y:
R43y = R4+R3y = R+R/3 = 4R/3.
Теперь резисторы R12y и R43y соединены параллельно. Их эквивалент .
К последовательно присоединен резистор R5y, таким образом, их эквивалент
.
Аналогично для группы резисторов R7..11 проводятся преобразования. Очевидно, что их эквивалентное сопротивление
R21 = R20 = R.
Таким образом, получились три последовательно соединенных резистора: R20, R6 и R21. Их эквивалентное сопротивление является полным сопротивлением цепи и составляет:
Rэ = R20+R6+R21 = R+R+R = 3R.
Симуляцию цепи, подтверждающую правильность приведенных расчетов, можно увидеть во вложении 3.
ЛЮБЫЕ тела получают тепло, если их температура меньше, чем у окружающей среды. Холодная вода тоже может отдавать тепло, если воздух вокруг имеет меньшую температуру или в ней плавает лед, а температура воды больше нуля хоть немного.
Это продолжается, пока не наступит тепловой баланс (пока температуры тел не сравняются).
Вы зимой проветрили комнату, в ней воздух с температурой <0.
Но проходит немного времени и в комнате опять тепло, т.к. стены, мебель и другие вещи в комнате отдали свое тепло холодному воздуху и теперь у всех тел одинаковая температура.
Мясо из морозилки размораживают в холодной воде, а то оно при варке будет жестким. Холодные напитки делают еще более холодными, бросив в них кубики льда. Мама учит не пить напитки сразу из холодильника, пусть постоят, согреются))
Вывод: холодная вода может получать тепло (из холодильника ее вынули и она стоит в теплой комнате), но та же самая вода будет отдавать тепло, если в нее бросить лед или подлить еще более холодную воду. Все зависит от температуры тела, с которым эта вода соприкасается.
3R
Объяснение:
Чтобы рассчитать подобную схему, ее нужно преобразовать.
Резисторы R2, R3 и R5 соединены треугольником. Преобразуем это соединение в эквивалентную звезду. Ввиду того, что все три резистора имеют одинаковые номиналы, сделать это нетрудно:
R2y = R3y = R5y = R/3 (см. вложения 1, 2).
Теперь резисторы R1 и R2y соединены последовательно, а их эквивалентное сопротивление составляет
R12y = R1+R2y = R+R/3 = 4R/3.
Аналогично для R4 и R3y:
R43y = R4+R3y = R+R/3 = 4R/3.
Теперь резисторы R12y и R43y соединены параллельно. Их эквивалент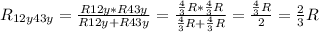
.
К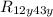
последовательно присоединен резистор R5y, таким образом, их эквивалент
Аналогично для группы резисторов R7..11 проводятся преобразования. Очевидно, что их эквивалентное сопротивление
R21 = R20 = R.
Таким образом, получились три последовательно соединенных резистора: R20, R6 и R21. Их эквивалентное сопротивление является полным сопротивлением цепи и составляет:
Rэ = R20+R6+R21 = R+R+R = 3R.
Симуляцию цепи, подтверждающую правильность приведенных расчетов, можно увидеть во вложении 3.