Тело движется в свободном падении, с нулевой начальной скоростью.
Значит движение тела задано следующим образом.
Пройденное расстояние вычисляется по формуле:
А расстояние пройденное за каждую конкретную секунду можно вычислить как расстояние, пройденного за n секунд минус расстояние, пройденного за n-1 секунд
Тогда
\: \:
4. Также воспользуемся терминологией, придуманной для задачи 2:
2. Тело пролетит:
4,9 м за первую секунду
14,7 м за вторую секунду
24,5 м ха третью секунду
4. ≈ 57.12 м
Объяснение:
№2. Дано:
Тело движется в свободном падении, с нулевой начальной скоростью.
Значит движение тела задано следующим образом.
Пройденное расстояние вычисляется по формуле:
А расстояние пройденное за каждую конкретную секунду можно вычислить как расстояние, пройденного за n секунд минус расстояние, пройденного за n-1 секунд
Тогда
\: \:
4. Также воспользуемся терминологией, придуманной для задачи 2:
Дано:
Найти: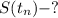
Далее см. рис.
Массы гирей равны 19,5 кг и 10,5 кг
Объяснение:
На концах нити, опрокинутой через неподвижный блок, подвешены две гири общей массой 30 кг. Система движется с ускорением 0,3g. Найти массы гирей.
m₁ + m₂ = 30 кг
а = 0,3g
m₁ - ?
m₂ - ?
Пусть m₁ > m₂, тогда гиря 1 движется вниз, а гиря 2 поднимается вверх.
Движение системы гирь описывается уравнениями
m₁a = m₁g - T (1)
m₂a = T - m₂g (2)
Здесь Т - сила натяжения нити
Из 2-го уравнения
Т = m₂a + m₂g
Подставим в 1-е уравнение
m₁a = m₁g - m₂a - m₂g
a (m₁ + m₂) = g (m₁ - m₂)
Подставим исходные данные
0.3g · 30 = g · (m₁ - m₂)
Имеем систему уравнений
m₁ - m₂ = 9 (3) складываем
m₁ + m₂ = 30 (4) уравнения
2m₁ = 39
m₁ = 19.5 (кг)
Из уравнения (4)
m₂ = 30 - m₁ = 30 - 19.5 = 10.5 (кг)
Проверим
Ускорение