Войти Регистрация Спроси ai-bota

КАКИЕ ИЗ УТВЕРЖДЕНИЙ ВЕРНЫЕ?

Показать ответ

Ответ:

cote18

21.12.2020 01:21

Частица, ускоренная разностью потенциалов 100В, движется в магнитном поле с индукцией 0,1 Тл по спирали радиуса 6,5 см с шагом 1 см. Найти отношение заряда частицы к ее массе. Пример решения задачи на тему движение заряда в магнитном поле по спирали

Электрон влетает со скоростью 1 Мм/с в магнитное поле под углом 60 градусов к силовым линиям. Напряженность магнитного поля 1,5 кА/м. Найти радиус и шаг спирали, по которой будет двигаться электрон.

Пример решения задачи на тему движение заряда в магнитном поле по спирали

Электрон движется в магнитном поле с индукцией 100 мкТл по спирали с радиусом 5 см и шагом 20 см. Найти скорость электрона.

Пример решения задачи на тему движение заряда в магнитном поле по спирали

Электрон, разогнанный разностью потенциалов 800В, движется в магнитном поле с индукцией 4,7 мТл по спирали с шагом 6 см. Найти радиус спирали.

Пример решения задачи на тему движение заряда в магнитном поле по спирали

Протон, разогнанный разностью потенциалов 300В, влетает в магнитное поле под углом 30 градусов к силовым линиям. Индукция магнитного поля 20 мТл. Найти радиус и шаг спирали, по которой будет двигаться протон.

Пример решения задачи на тему движение заряда в магнитном поле по спирали

Электрон, разогнанный разностью потенциалов 6 кВ, влетает в магнитное поле под углом 30 градусов к силовым линиям. Индукция магнитного поля 13 мТл. Найти радиус и шаг спирали, по которой будет двигаться электрон.

Пример решения задачи на тему движение заряда в магнитном поле по спирали

Альфа-частица, разогнанная разностью потенциалов U, влетает в магнитное поле под углом к силовым линиям. Индукция магнитного поля 50 мТл. Hадиус и шаг спирали - траектории частицы - соответственно 5 см и 1 см. Определить разность потенциалов U.

Пример решения задачи на тему движение заряда в магнитном поле по спирали

Пример решения задачи на тему движение заряда в магнитном поле по спирали

Пример решения задачи на тему движение заряда в магнитном поле по спирали

Электрон влетает со скоростью 1 Мм/с в магнитное поле под углом 30 градусов к силовым линиям. Индукция магнитного поля 1,2 мТл. Найти радиус и шаг спирали, по которой будет двигаться электрон.

Пример решения задачи на тему движение заряда в магнитном поле по спирали

Электрон влетает со скоростью 6 Мм/с в магнитное поле под углом 30 градусов к силовым линиям. Индукция магнитного поля 1,0 мТл. Найти радиус и шаг спирали, по которой будет двигаться электрон.

0,0(0 оценок)

Ответ:

nilovaekaterin

07.03.2020 00:11

570 мкТл; 6,6 мкТл; 1,11 мкТл; 0,35 мкТл; 0,15 мкТл

454 А/м; 5,3 А/м; 0,88 А/м; 0,28 А/м; 0,12 А/м

Объяснение:

Здравствуйте за интересную и сложную задачу.

Из соображений симметрии найдем индукцию магнитного поля в точке А (первый рисунок), создаваемую только одним проводником. Как нетрудно убедиться, результирующее поле от всех 4 проводников в точек А будет равно

$B_0=4B_x=4Bcos\phi$

Найдем поле B, создаваемое одной стороной квадрата в точке А. Для этого несколько изменим наш угол зрения (второй рисунок).

Закон Био-Савара-Лапласа для малого элемента тока dl имеет вид

$dB=\frac{\mu_0I}{4\pi }\frac{sin\alpha }{r^2}dl$

Выразим малый элемент длины проводника dl через угол и расстояние от проводника до точки наблюдения

$r=\frac{b}{sin\alpha }$

$dl=\frac{rd\alpha }{sin\alpha } =\frac{bd\alpha }{sin^2\alpha }$

С учетом этого

$dB=\frac{\mu_0I}{4\pi } \frac{sin\alpha }{b}d\alpha$

Магнитную индукцию, создаваемую всем отрезком проводника легко найти, взяв соответствующий определенный интеграл

$B=\frac{\mu_0I}{4\pi b} \int\limits^{\alpha_2 }_{\alpha_1 } {sin\alpha } \, d\alpha =-\frac{\mu_0I}{4\pi b} cos\alpha |_{\alpha _1} ^{\alpha_2}=\frac{\mu_0I}{4\pi b}(cos\alpha _1-cos\alpha_2 )$

Возвращаемся к нашей пространственной задаче. Расстояние b, очевидно, равно (далее я буду оперировать числами, иначе формулы обрастут переменными как снежный ком)

$b=\sqrt{\frac{a^2}{4} +x^2}=\sqrt{\frac{0.1^2}{4}+x^2 }=\sqrt{0.0025+x^2}$

Углы α₁ и α₂, а точнее сразу их косинусы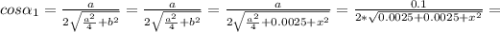 $cos\alpha _1=\frac{a}{2\sqrt{\frac{a^2}{4} +b^2} }= \frac{a}{2\sqrt{\frac{a^2}{4} +b^2} }=\frac{a}{2\sqrt{\frac{a^2}{4} +0.0025+x^2} }=\frac{0.1}{2*\sqrt{0.0025+0.0025+x^2} }=$

$=\frac{0.05}{\sqrt{0.005+x^2} }$

$cos\alpha _2=cos(\pi -\alpha_1 )=-cos\alpha _1=\frac{-0.05}{\sqrt{0.005+x^2} }$

Магнитное поле, создаваемое одной стороной квадрата в точке А

$B=\frac{\mu_0I}{4\pi \sqrt{0.0025+x^2} }\frac{0.1}{\sqrt{0.005+x^2} }$

Проекция вектора B на ось х

$B_x=Bcos\phi=B\frac{a}{2b}=B\frac{a}{2\sqrt{0.0025+x^2} }=B\frac{0.05}{\sqrt{0.0025+x^2} } =$

$=\frac{\mu_0I}{4\pi \sqrt{0.0025+x^2} }\frac{0.1}{\sqrt{0.005+x^2} }\frac{0.05}{\sqrt{0.0025+x^2} } =\frac{0.005\mu_0I}{4\pi (0.0025+x^2)\sqrt{0.005+x^2} }$

Результирующее поле со стороны всего квадрата будет в 4 раза больше

$B_0=\frac{0.02\mu_0I}{4\pi (0.0025+x^2)\sqrt{0.005+x^2} }$

Вот, почти все. Осталось только подставить в последнюю формулу ваши значения координаты х и произвести расчеты

$B_0(0)=\frac{0.02*4\pi *10^-^7*5}{4\pi *0.0025*0.007} =0.00057$ Тл

$B_0(0.1)=\frac{0.02*4\pi *10^-^7*5}{4\pi* 0.0125*0.122}= 6.6*10^-^6$ Тл

$B_0(0.2)=\frac{0.02*4\pi *10^-^7*5}{4\pi* 0.0425*0.212}=1.11*10^-^6$ Тл

$B_0(0.3)=\frac{0.02*4\pi *10^-^7*5}{4\pi* 0.0925*0.31}=3.49*10^-^7$ Тл

$B_0(0.4)=\frac{0.02*4\pi *10^-^7*5}{4\pi* 0.163*0.41}=1.5*10^-^7$ Тл

Напряженность магнитного поля легко найти из соотношения

$H_0=\frac{B}{\mu_0}$

Тогда

H_0(0)=454 А/м

H_0(0.1)=5.3 А/м

H_0(0.2)=0.88 А/м

H_0(0.3)=0.28 А/м

H_0(0.4)=0.12 А/м.

решить. Какими формулами и теоремами пользовались при решении?

решить. Какими формулами и теоремами пользовались при решении?

0,0(0 оценок)

Популярные вопросы: Физика

nikonova1977

24.04.2022 13:11

Какой выигрыш в силе дает сочетание двух блоков (подвижного и неподвижного)? Используя эту систему блоков , найти какая сила необходима для подъёма груза весом...

kenzhe1

21.02.2023 08:42

Cipник масою 0,09г лежить на поверхні води. 3 яким прискоренням він почне рухатись, якщо з одного боку торкнутись поверхні води милом. Довжина сірника-4см....

komarenko

27.10.2022 23:53

Груз весом Р=1000Н поднимают на высоту h=4м по наклонной плоскости длиной L=8м прикладывая силу F=300Н А) Сделай рисунок. ...

yaroshenkopoli

22.07.2021 23:18

надо 3. Птичка колибри массой 2 г при полете достигает скорости 0,05 км/с. Определите кинетическую энергиюдвижения этой птички.4. В момент вылета из ствола пружинного...

nata960

12.02.2021 01:48

Вычислите среднюю скорость движения человека,если на прохождение первой части пути он затратил 20 мин, на прохождение второй-40 мин , а общий путь, пройденный человеком,составил...

valnov24200105oxnmv8

12.02.2021 01:48

Объясните , что такое инерция? и назовите примеры инерции в быту....

Igor171717

12.02.2021 01:48

Напиши сочинение на тему плюсы и минусы инерции...

Ксюхахаха

29.06.2021 06:40

На скільки градусів нагріється кусок міді масою 500 г, якщо йому надати таку ж кількість теплоти, котра піде на нагрівання води масою 200г від 10°с до 60°с...

LoveSammer

01.05.2022 07:43

Упосудину з водою, маса якої 150 г, а температура 16 °с, додали воду масою 50 г при температурі 80°с. визначте температуру суміші....

sallga

25.12.2020 13:48

Почему при погружении в воду тело подвешенное к динамометру показывания динамо метра уменьшаются...

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку