По определению, вес – это сила, с которой тело давит на опору (или подвес, в данном случае – опору). По III Закону Ньютона, эта сила равна по модулю силе реакции опоры , которая в свою очередь равна по модулю поперечной к опоре составляющей силы тяжести (по II Закону Ньютона, поскольку поперечную к поверхности составляющую ускорения санок мы считаем равной нулю):
.
В случае горизонтальной опоры, т.е. когда мальчик на санках расположен на горизонтальной плоскости:
.
В случае, когда мальчик на санках находится на горке, острый угол между плоскосью горки и горизонталью равен углу отклонения поперечной составляющей от вертикали, откуда:
;
.
Теперь найдём отношение:
.
* В решении мы пренебрегаем силой трения. Чем больше трение, тем сильнее вес будет отличаться от реакции опоры. В частности, если трение не будут позволять санкам съезжать (грязный мокрый снег в перемежку с землёй), то вес снова окажется равным силе тяжести. Чтобы учитывать трение, нужно знать его коэффициент , который в условии не дан, так что мы считаем, что .
Объяснение:
По определению, вес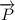 – это сила, с которой тело давит на опору (или подвес, в данном случае – опору). По III Закону Ньютона, эта сила равна по модулю силе реакции опоры
– это сила, с которой тело давит на опору (или подвес, в данном случае – опору). По III Закону Ньютона, эта сила равна по модулю силе реакции опоры 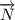 , которая в свою очередь равна по модулю поперечной к опоре составляющей силы тяжести
, которая в свою очередь равна по модулю поперечной к опоре составляющей силы тяжести 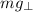 (по II Закону Ньютона, поскольку поперечную к поверхности составляющую ускорения санок мы считаем равной нулю):
(по II Закону Ньютона, поскольку поперечную к поверхности составляющую ускорения санок мы считаем равной нулю):
В случае горизонтальной опоры, т.е. когда мальчик на санках расположен на горизонтальной плоскости:
В случае, когда мальчик на санках находится на горке, острый угол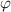 между плоскосью горки и горизонталью равен углу отклонения поперечной составляющей от вертикали, откуда:
между плоскосью горки и горизонталью равен углу отклонения поперечной составляющей от вертикали, откуда:
Теперь найдём отношение:
* В решении мы пренебрегаем силой трения. Чем больше трение, тем сильнее вес будет отличаться от реакции опоры. В частности, если трение не будут позволять санкам съезжать (грязный мокрый снег в перемежку с землёй), то вес снова окажется равным силе тяжести. Чтобы учитывать трение, нужно знать его коэффициент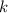 , который в условии не дан, так что мы считаем, что
, который в условии не дан, так что мы считаем, что 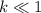 .
.
Объяснение:
Все мешки одинакового объема V (пусть данный объем = 1).
Тогда для смеси
V= Vг+Vk (Vг - объем гороха в смеси Vk- Объем кукурузы в смеси)
Отсюда
Vг= V - Vk = 1 - Vk
Плотность кукурузы рк и плотность гороха рг (плотность на мешок) можно найти взвесив мешки только с горохом и только с кукурузой.
рк =mk/V = mk /1
pг =mг / V = mг / 1
тогда для смеси (mc - масса смеси - взвешен мешок со смесью)
mc = Vk*рк + Vг*pг = Vk * mk + Vг * mг
mc = (Vk * mk) + ((1 - Vk) * mг)
mc = Vk * mk + mг - Vk * mг
mc - mг = Vk *( mk - mг)
(mc - mг) / ( mk - mг) = Vk
Vk * 100% - получим в процентах
тогда для гороха
Vг= (1 - Vk) * 100%
пример: пусть кукурузный мешок имеет массу mk=100 кг, мешок гороха mг= 150 кг, мешок смеси mc=120 кг.
Vk= (mc - mг) / ( mk - mг) = (120-150) / (100-150)= - 30 / (- 50) = 0,6
Vk = 0,6*100%=60 % кукурузы
Vг= (1 - 0,6) * 100% = 40 % - гороха