Теория распространения упругих (сейсмических) волн базируется на теории упругости, так как геологические среды в первом приближении можно считать упругими. Поэтому напомним основные определения и законы теории упругости применительно к однородным изотропным средам.
Установлено, что под действием внешних нагрузок жидкие и газообразные тела изменяют свои объем и форму, деформируются. При деформации частицы тела смещаются относительно друг друга и исходного положения. Величина и направление перемещений определяются величиной и характером внешних сил и свойствами тела. Положение частиц тела после деформации можно найти, если известен вектор перемещений U(х, у, z), ..При этом изменится длина его ребер, а прежде прямые углы между соответствующими ребрами станут тупыми или острыми. Количественной мерой деформации являются относительные удлинения ребер малого параллелепипеда и абсолютное изменение углов относительно 90°. Таким образом, деформация полностью описывается шестью компонентами. Три первые компоненты называются продольными (нормальными) деформациями, три последние — сдвиговыми.
При снятии нагрузки частицы тела могут вернуться или не вернуться в исходное положение. В первом случае говорят об обратимых, а во втором о необратимых деформациях. Тела, в которых развиваются только обратимые деформации, называют упругими. Тела, в которых развиваются только необратимые деформации.
При деформации в упругом теле возникают внутренние напряжения, обусловленные упругим взаимодействием между частицами тела. На каждую площадку малого размера, мысленно выделяемую в теле, действуют напряжения, имеющие в общем случае одну составляющую, перпендикулярную к площадке, — нормальное напряжение, и две, направленные вдоль площадки, называемые сдвиговыми напряжениями. Три компоненты напряжения задаются с шести компонент тензора напряжения. Эти шесть компонент связаны с шестью компонентами малых деформаций законом Гука.
При одноосном сжатии (растяжении) призмы из твердого тела относительное изменение ее длины вдоль направления действующего напряжения выражается соотношением
где Ω — величина внешней нагрузки; Е — модуль Юнга; Л — длина призмы; ΔЛ — изменение длины.
Опыт показывает, что удлинение призмы всегда сопровождается сокращением ее поперечных размеров a и b на Δa и Δb. Для изотропных тел ΔЛ/Л, Δa/a, Δb/b и (Δa/a)/(Δb/b) = Δ остаются неизменными, независимо от того, каким образом была ориентирована призма в породе, где Δ — коэффициент Пуассона.
Модуль Юнга (E) и коэффициент Пуассона (Δ) полностью определяют упругие свойства таких тел. Для анизотропных сред при неизменной осевой нагрузке относительные удлинения ребер призмы будут зависеть от того, как была ориентирована ось призмы в породе, иными словами, упругие свойства зависят от направления внешних нагрузок. Изотропные тела можно также описать с упругих констант Ламэ — модуля сжатия (λ) и модуля сдвига (µ). Эти модули однозначно связаны с модулем Юнга (Е) и коэффициентом Пуассона (Δ):
При всестороннем сжатии упругих тел, например, путем повышения давления жидкости, в которой расположен образец, объем тел уменьшается. Относительное изменение объема (ΔV/V) при этом линейно связано с давлением:
Коэффициент (kc) называют модулем всестороннего сжатия. Для изотропных тел связь между kc, λ и μ имеет вид
В жидкостях и газах μ = 0 и kc = λ.
Если упругие свойства тел не изменяются при переходе от точки к точке тела, то такие тела называют однородными. В противном случае тело называют неоднородным. В неоднородных изотропных телах λ, μ и kc — функции координат.
При деформации упругого тела под действием внешней нагрузки размеры тела изменяются, например, стержень сжимается. Если при снятии внешней нагрузки вся потенциальная энергия переходит в кинетическую, то тело называют идеально-упругим. Если же часть энергии уходит на необратимые процессы, например, превращается в тепло, то тело называют вязко-упругим, неидеально-упругим.
тел деформироваться является причиной того, что напряжение от зоны действия внешней нагрузки распространяется на все области тела с конечной скоростью, определяемой упругими модулями и плотностью. Распространяющееся в упругом теле напряжение порождает деформации — перемещения частиц тела, которые можно измерить. Наблюдения за перемещением частиц тела позволяют экспериментально измерять скорости распространения упругих волн и выявлять различия в физических свойствах горных пород или их состоянии.
1. Тело свободно падает с высоты 39,2 м. За какое время тело пройдет: а) первый метр своего пути; б) последний метр своего пути? Чему равна средняя скорость на второй половине пути?
Дано:
м
м/с²
Найти: а) б)
Решение. а) Следует определить время , за которое тело пройдет расстояние, равное м.
Направим ось в сторону падения тела. Воспользуемся формулой:
Перейдем от проекций к модулям:
Тогда
б) Время , за которое тело пройдет расстояние, равное
Полное время:
Тогда последний метр своего пути тело пройдет за:
Следует определить среднюю скорость на второй половине пути.
Длина первой половины пути –
Тогда можно записать, что , где – время прохождения телом первой половины пути, его можно найти:
Тогда время на второй половине пути:
Чтобы определить среднюю путевую скорость, нужно разделить весь путь на все время:
Определим значение искомых величин:
а)
б)
м/с
ответ: а) 0,45 с; б) 0,04 с; 24 м/с.
2. Тело, которое свободно падает без начальной скорости, за последнюю секунду движения проходит всего пути. Определите путь, пройденный телом за время падения.
Дано:
м/с²
Найти:
Решение. Высота падения тела:
Тогда путь где – путь, пройденный за время , то есть
Тогда
Имеем:
Сократим обе части уравнения на
Таким образом, тело весь путь за 2,37 с. Тогда
м
ответ: 28 м.
3. Тело свободно падает с высоты 60 м. Определите его перемещение за последнюю секунду падения.
Объяснение:
Теория распространения упругих (сейсмических) волн базируется на теории упругости, так как геологические среды в первом приближении можно считать упругими. Поэтому напомним основные определения и законы теории упругости применительно к однородным изотропным средам.
Установлено, что под действием внешних нагрузок жидкие и газообразные тела изменяют свои объем и форму, деформируются. При деформации частицы тела смещаются относительно друг друга и исходного положения. Величина и направление перемещений определяются величиной и характером внешних сил и свойствами тела. Положение частиц тела после деформации можно найти, если известен вектор перемещений U(х, у, z), ..При этом изменится длина его ребер, а прежде прямые углы между соответствующими ребрами станут тупыми или острыми. Количественной мерой деформации являются относительные удлинения ребер малого параллелепипеда и абсолютное изменение углов относительно 90°. Таким образом, деформация полностью описывается шестью компонентами. Три первые компоненты называются продольными (нормальными) деформациями, три последние — сдвиговыми.
При снятии нагрузки частицы тела могут вернуться или не вернуться в исходное положение. В первом случае говорят об обратимых, а во втором о необратимых деформациях. Тела, в которых развиваются только обратимые деформации, называют упругими. Тела, в которых развиваются только необратимые деформации.
При деформации в упругом теле возникают внутренние напряжения, обусловленные упругим взаимодействием между частицами тела. На каждую площадку малого размера, мысленно выделяемую в теле, действуют напряжения, имеющие в общем случае одну составляющую, перпендикулярную к площадке, — нормальное напряжение, и две, направленные вдоль площадки, называемые сдвиговыми напряжениями. Три компоненты напряжения задаются с шести компонент тензора напряжения. Эти шесть компонент связаны с шестью компонентами малых деформаций законом Гука.
При одноосном сжатии (растяжении) призмы из твердого тела относительное изменение ее длины вдоль направления действующего напряжения выражается соотношением
где Ω — величина внешней нагрузки; Е — модуль Юнга; Л — длина призмы; ΔЛ — изменение длины.
Опыт показывает, что удлинение призмы всегда сопровождается сокращением ее поперечных размеров a и b на Δa и Δb. Для изотропных тел ΔЛ/Л, Δa/a, Δb/b и (Δa/a)/(Δb/b) = Δ остаются неизменными, независимо от того, каким образом была ориентирована призма в породе, где Δ — коэффициент Пуассона.
Модуль Юнга (E) и коэффициент Пуассона (Δ) полностью определяют упругие свойства таких тел. Для анизотропных сред при неизменной осевой нагрузке относительные удлинения ребер призмы будут зависеть от того, как была ориентирована ось призмы в породе, иными словами, упругие свойства зависят от направления внешних нагрузок. Изотропные тела можно также описать с упругих констант Ламэ — модуля сжатия (λ) и модуля сдвига (µ). Эти модули однозначно связаны с модулем Юнга (Е) и коэффициентом Пуассона (Δ):
При всестороннем сжатии упругих тел, например, путем повышения давления жидкости, в которой расположен образец, объем тел уменьшается. Относительное изменение объема (ΔV/V) при этом линейно связано с давлением:
Коэффициент (kc) называют модулем всестороннего сжатия. Для изотропных тел связь между kc, λ и μ имеет вид
В жидкостях и газах μ = 0 и kc = λ.
Если упругие свойства тел не изменяются при переходе от точки к точке тела, то такие тела называют однородными. В противном случае тело называют неоднородным. В неоднородных изотропных телах λ, μ и kc — функции координат.
При деформации упругого тела под действием внешней нагрузки размеры тела изменяются, например, стержень сжимается. Если при снятии внешней нагрузки вся потенциальная энергия переходит в кинетическую, то тело называют идеально-упругим. Если же часть энергии уходит на необратимые процессы, например, превращается в тепло, то тело называют вязко-упругим, неидеально-упругим.
тел деформироваться является причиной того, что напряжение от зоны действия внешней нагрузки распространяется на все области тела с конечной скоростью, определяемой упругими модулями и плотностью. Распространяющееся в упругом теле напряжение порождает деформации — перемещения частиц тела, которые можно измерить. Наблюдения за перемещением частиц тела позволяют экспериментально измерять скорости распространения упругих волн и выявлять различия в физических свойствах горных пород или их состоянии.
4.2.2. УПРУГИЕ ВОЛНЫ В БЕЗГРАНИЧНЫ
1. Тело свободно падает с высоты 39,2 м. За какое время тело пройдет: а) первый метр своего пути; б) последний метр своего пути? Чему равна средняя скорость на второй половине пути?
Дано:
Найти: а) б)
б) 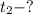
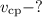
Решение. а) Следует определить время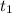 , за которое тело пройдет расстояние, равное
, за которое тело пройдет расстояние, равное 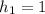 м.
м.
Направим ось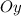 в сторону падения тела. Воспользуемся формулой:
в сторону падения тела. Воспользуемся формулой:
Перейдем от проекций к модулям:
Тогда
б) Время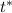 , за которое тело пройдет расстояние, равное
, за которое тело пройдет расстояние, равное 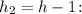
Полное время: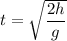
Тогда последний метр своего пути тело пройдет за: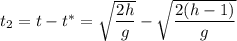
Следует определить среднюю скорость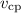 на второй половине пути.
на второй половине пути.
Длина первой половины пути –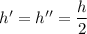
Тогда можно записать, что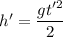 , где
, где 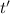 – время прохождения телом первой половины пути, его можно найти:
– время прохождения телом первой половины пути, его можно найти: 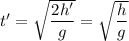
Тогда время на второй половине пути: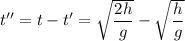
Чтобы определить среднюю путевую скорость, нужно разделить весь путь на все время:
Определим значение искомых величин:
а)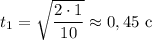
б)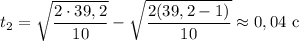
ответ: а) 0,45 с; б) 0,04 с; 24 м/с.
2. Тело, которое свободно падает без начальной скорости, за последнюю секунду движения проходит всего пути. Определите путь, пройденный телом за время падения.
всего пути. Определите путь, пройденный телом за время падения.
Дано:
Найти: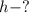
Решение. Высота падения тела: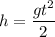
Тогда путь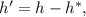 где
где 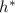 – путь, пройденный за время
– путь, пройденный за время  , то есть
, то есть 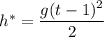
Тогда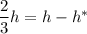
Имеем: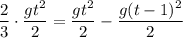
Сократим обе части уравнения на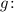
Таким образом, тело весь путь за 2,37 с. Тогда
ответ: 28 м.
3. Тело свободно падает с высоты 60 м. Определите его перемещение за последнюю секунду падения.
Дано:
Найти: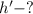
Решение. Полное время: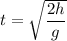
Пройденный путь тела за секунд:
секунд:
Имеем:
Определим значение искомой величины:
ответ: 30 м.