Какой механизм представляет собой тормоз?

Дано:

Масса угля: m₁ = 200 г = 0,2 кг.

Удельная теплота сгорания угля: q = 20,5 МДж/кг = 20,5 × 10⁶ Дж/кг.

Объём воды: V₂ = 2 м³.

Плотность воды: ρ₂ = 1000 кг/м³.

Начальная температура: t₁ = 0 °C.

Конечная температура: t₂ = 70 °C.

Потери при нагревании воды: k = 80% = 0,8.

Удельная теплоёмкость воды: с = 4200 Дж/(кг × °C).

Найти нужно, достаточно ли теплоты, то есть Q₁ ≥ Q₂ - ?

Решение:

0. Теплота, полученная от сгорания угля тратится на нагревание воды, возможно с избытком, поэтому теплота сгорания должна быть не меньше теплоты, необходимой для нагревания.

1. Теплота сгорания угля (без учёта потерь): Q₁' = qm₁.

2. Масса воды: m₂ = ρ₂V₂.

3. Теплота нагревания воды: Q₂ = cm₂(t₂ - t₁) = cρ₂V₂(t₂ - t₁).

4. Т. к. при нагревании воды мы теряем 80% энергии от сгорания угля, то КПД сгорания угля: η = 1 - k.

5. Сгорание угля с учётом КПД: Q₁ = ηQ₁' = ηqm₁ = (1 - k)qm₁.

Найдём численные значения Q₁ и Q₂.

Q₁ = (1 - 0,8) × 20,5 × 10⁶ × 0,2 = 820000 (Дж).

Q₂ = 4200 × 1000 × 2 × (70 - 0) = 588000000 (Дж).

Так как Q₁ < Q₂, то полученной теплоты будет недостаточно.

ответ: нет.

Дано:

Время подъёма на определённую высоту: t₁ = 2 c.

Высота подъёма за 2 с: h₁ = 100 м.

Ускорение свободного падения: g = 10 м/с².

Найти максимальную высоту и время подъёма на неё: h, t - ?

Решение:

1. Уравнение зависимости высоты от времени при движении против силы притяжения для высоты h₁: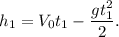

2. Выразим начальную скорость из (1):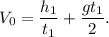

Для упрощения вычислений, найдём численное значение начальной скорости сейчас:

(м/с).

3. Запишем уравнение зависимости скорости от времени при движении против силы притяжения: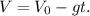

4. На максимальной высоте скорость станет равна нулю, V = 0. Выразим время подъёма на максимальную высоту из (3):

5. Зная время подъёма, легко найдём максимальную высоту подъёма: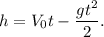

Численно получим: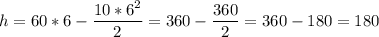

(c).

(м).

ответ: 6 с; 180 м.