Какую горизонтальную скорость должен иметь бомбардировщик при сбрасывании с высоты 4500 м, чтобы она упала на расстоянии 6 км от места бросания? И что бы было написано дано

Объяснение:

Дано:

d = 30,3 см

H = h

Δd = 2,8 см

Г₁ = 1,2

Куда передвинули  предмет?

На сколько передвинули  (Δf) ?

1)

Размеры предмета и его изображения одинаковы, когда предмет находится на двойном фокусном расстоянии от линзы. Расстояние до изображения f = d = 30,3 см.

Отсюда:

2·F = d

F = d/2 = 30,3 / 2 = 15,15 см -  фокус линзы.

2)

Передвинем предмет на Δd к линзе:

Тогда:

d₁ = d - Δd = 30,3 - 2,8 = 27,5 см

Найдем новое расстояние до изображения из формулы линзы:

1 / F = 1/d₁ + 1/f₁

1/f₁ = 1 / F - 1 / d₁

f₁ = d₁·F / (d₁ - F)

f₁ = 27,5·15,15 / (27,5-15,15) ≈ 33,7 см

То есть экран отодвинули от линзы  вправо на:

Δf = f₁ - f = 33,7 - 30,3 = 3,4 см

Проверим:

Г₁ = f₁/d₁ = 33,7 / 27,5 ≈ 1,2  

Задача решена верно!

Массу тела следует увеличить в 9 раз, чтобы кинетическая энергия этого тела увеличилась в 9 раз.

Объяснение:

Запишем формулу кинетической энергии тела:

Запишем данную формулу для нашего первого случая:

(1)

Для второго случая:

Но у нас известно условие, что кинетическая энергия во втором случае увеличится в 9 раз, то есть , подставляя это условие во вторую формулу, получаем:

Теперь выразим из этой формулы :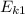

(2)

Приравниваем (1) и (2), получаем соотношение масс, откуда выражаем :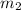

Следовательно, массу тела следует увеличить в 9 раз.