Юпи́тер — пятая планета от Солнца, крупнейшая в Солнечной системе. Наряду с Сатурном, Ураном и Нептуном Юпитер классифицируется как газовый гигант.
Планета была известна людям с глубокой древности, что нашло своё отражение в мифологии и религиозных верованиях различных культур: месопотамской, вавилонской, греческой и других. Современное название Юпитера происходит от имени древнеримского верховного бога-громовержца.
Ряд атмосферных явлений на Юпитере: штормы, молнии, полярные сияния, — имеет масштабы, на порядки превосходящие земные. Примечательным образованием в атмосфере является Большое красное пятно — гигантский шторм, известный с XVII века.
Юпитер имеет, по крайней мере, 67 спутников, самые крупные из которых — Ио, Европа, Ганимед и Каллисто — были открыты Галилео Галилеем в 1610 году.
Исследования Юпитера проводятся при наземных и орбитальных телескопов; с 1970-х годов к планете было отправлено 8 межпланетных аппаратов НАСА: «Пионеры», «Вояджеры», «Галилео» и другие.
Во время великих противостояний (одно из которых происходило в сентябре 2010 года) Юпитер виден невооружённым глазом как один из самых ярких объектов на ночном небосклоне после Луны и Венеры. Диск и спутники Юпитера являются популярными объектами наблюдения для астрономов-любителей , сделавших ряд открытий (например, кометы Шумейкеров-Леви, которая столкнулась с Юпитером в 1994 году, или исчезновения Южного экваториального пояса Юпитера в 2010 году) .
1.) Давление- векторная физическая величина, численно равная силе, действующей на единицу площади поверхности. ( для твердых тел)
Гидростатическое давление — давление столба жидкости над условным уровнем. ( для жидкостей)
2.) Давление твёрдых тел зависит от силы (F) и площади поверхности (S), на которую действует эта сила.
Давление жидкости зависит от плотности данной жидкости (PO) и столба жидкости над условным уровнем (h).
3.) Любое давление измеряется в СИ в Паскалях. (Па)
Формула давления твёрдых тел: p=F/S, где F- сила, S- площадь поверхности, на которую действует эта сила.
Формула давления жидкости: p= POgh, где PO- плотность жидкости, g- ускорение свободного падения, h- высота столба жидкости над условным уровнем.
4.) Закон Паскаля в словесном виде: Давление, производимое на жидкость или газ, передается в любую точку без изменений во всех направлениях.
Закон Паскаля в виде формулы: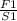 =
=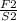
5.) Работа- это векторная физическая величина, численно равная произведению модуля силы, действующей на тело на модуль его перемещения.
6.) Мощность- скалярная физическая величина, показывающая, какую работу совершает тело за единицу времени.
7.) Формула работы: A= FS, где F- сила, S- перемещение.
Формула мощности: N= A/t, где A- работа, t- время, за которое эта работа была совершена.
8.) Энергия- это скалярная физическая величина, характеризующая тела совершать механическую работу.
9.) Виды энергии: кинетическая (движении тела), потенциальная (тело над землёй/ упруго- деформированное тело), внутренняя.
Планета была известна людям с глубокой древности, что нашло своё отражение в мифологии и религиозных верованиях различных культур: месопотамской, вавилонской, греческой и других. Современное название Юпитера происходит от имени древнеримского верховного бога-громовержца.
Ряд атмосферных явлений на Юпитере: штормы, молнии, полярные сияния, — имеет масштабы, на порядки превосходящие земные. Примечательным образованием в атмосфере является Большое красное пятно — гигантский шторм, известный с XVII века.
Юпитер имеет, по крайней мере, 67 спутников, самые крупные из которых — Ио, Европа, Ганимед и Каллисто — были открыты Галилео Галилеем в 1610 году.
Исследования Юпитера проводятся при наземных и орбитальных телескопов; с 1970-х годов к планете было отправлено 8 межпланетных аппаратов НАСА: «Пионеры», «Вояджеры», «Галилео» и другие.
Во время великих противостояний (одно из которых происходило в сентябре 2010 года) Юпитер виден невооружённым глазом как один из самых ярких объектов на ночном небосклоне после Луны и Венеры. Диск и спутники Юпитера являются популярными объектами наблюдения для астрономов-любителей , сделавших ряд открытий (например, кометы Шумейкеров-Леви, которая столкнулась с Юпитером в 1994 году, или исчезновения Южного экваториального пояса Юпитера в 2010 году) .