Известны несколько гипотез природы магнитного поля Земли, но ни одна из них неявляется убедительной. Это относится и к природе электрического поля Земли.В предлагаемой статье обсуждается связь магнитного поля Земли с движениемЛуны вокруг Земли, а также связь электрического поля Земли с веществом Земли.Общеизвестно, что магнитное поле является следствием движенияэлектрических зарядов; то есть, следствием электрического тока.Напряженность магнитного поля Н в центре кругового витка с токомопределяется зависимостьюA м2RIH , (1)где R – радиус кругового витка, по которому течет ток І [1, стр. 210].Положим, что Луна, как и Земля, имеет электрический заряд, движениекоторого создавать магнитное поле. Тогда в зависимость (1)следует в явной форме ввести единицу пути движения Луны вокруг Земли –1 оборот или 1 виток; то естьA вит м1вит2RIH . (2)Обозначим следующие известные величины:1. Один виток Луны вокруг Земли происходит за 27,3 суток [2, стр. 93]или в единицах системы СИ – за 2,4106секунды, то есть1 вит = 27,3 сут = 2,4106с. (3)2. Средний радиус орбиты-витка Луны вокруг Земли составляетвеличину 384400 км [2, стр. 88] или в единицах системы СИ3,84 10 м8 R . (4)3. Напряженность магнитного поля Земли на средних широтах –широте Киева равна 0,17 эрстед [3, стр. 122] или в единицах системы СИ –13,5 А/м [4, стр. 257]; то естьH 0,17Э 13,5 A м. (5)Тогда, на основе (2), с учетом (3), (4) и (5), получим4,32 10 А с2,4 1013,5 2 3,84 101вит2 368 H RI, (6)где І – электрический ток, создаваемый электрическим зарядом Луны.Прокомментируем размерность ампер/секунда результата (6).В отличие от системы единиц СГС, в которой единица электрическоготока определяется как движение единицы электрического заряда за единицувремени, в системе единиц СИ единица электрического тока – ампер естьосновная единица со следующим определением:
13. Поле в сферическом конденсаторе создаётся только зарядами внутренней обкладки, а в диэлектриках – ещё и связанным зарядом.
Для определённости, пусть ,
для и для ;
;
;
;
;
;
;
;
;
10. Энергия взаимодействия левого заряда с центральным: ;
энергия взаимодействия правого заряда с центральным: ;
энергия взаимодействия левого заряда с правым: ;
Полная энергия взимодействия: ;
9. Из Теоремы Гаусса, поле бесконечной струны может быть вычислено, как , где – линейное распределение заряда по струне, удельное к длине.
В любой электростатической системе потенциал представляется функцией, противоположной к первообразной напряжённости поля, а значит, для бесконечной струны потенциал может быть вычислен, как: , где – радиус нулевого потенциала, который выбирается свободно (но не меняется в ходе решения задачи), и чаще всего за радиус нулевого потенциала уднобно принять радиус струны.
Потенциальная энергия взаимодействия куска второй струны, находящейся на расстоянии от первой .
Потенциальная энергия взаимодействия второй струны, находящейся от первой на расстоянии , удельная к длине: .
Потенциальная энергия взаимодействия второй струны, находящейся от первой на расстоянии , удельная к длине: .
Работа, удельная к длине, совершаемая полем при увеличении расстояния между струнами от до равна разности потенциальных энергий этих конфигураций, удельных к длине:
;
;
Работа, удельная к длине, совершаемая полем при увеличении расстояния между струнами от до будет равна: ;
13)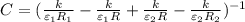
10)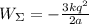
9) 1.843 мДж/м
Объяснение:
13. Поле в сферическом конденсаторе создаётся только зарядами внутренней обкладки, а в диэлектриках – ещё и связанным зарядом.
Для определённости, пусть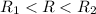 ,
,
10. Энергия взаимодействия левого заряда с центральным: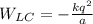 ;
;
энергия взаимодействия правого заряда с центральным: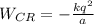 ;
;
энергия взаимодействия левого заряда с правым: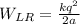 ;
;
Полная энергия взимодействия: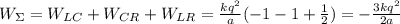 ;
;
9. Из Теоремы Гаусса, поле бесконечной струны может быть вычислено, как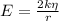 , где
, где 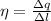 – линейное распределение заряда по струне, удельное к длине.
– линейное распределение заряда по струне, удельное к длине.
В любой электростатической системе потенциал представляется функцией, противоположной к первообразной напряжённости поля, а значит, для бесконечной струны потенциал может быть вычислен, как: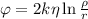 , где
, где 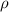 – радиус нулевого потенциала, который выбирается свободно (но не меняется в ходе решения задачи), и чаще всего за радиус
– радиус нулевого потенциала, который выбирается свободно (но не меняется в ходе решения задачи), и чаще всего за радиус 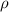 нулевого потенциала уднобно принять радиус струны.
нулевого потенциала уднобно принять радиус струны.
Потенциальная энергия взаимодействия куска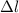 второй струны, находящейся на расстоянии
второй струны, находящейся на расстоянии 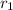 от первой
от первой 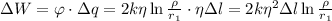 .
.
Потенциальная энергия взаимодействия второй струны, находящейся от первой на расстоянии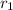 , удельная к длине:
, удельная к длине: 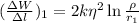 .
.
Потенциальная энергия взаимодействия второй струны, находящейся от первой на расстоянии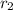 , удельная к длине:
, удельная к длине: 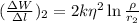 .
.
Работа, удельная к длине, совершаемая полем при увеличении расстояния между струнами от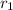 до
до 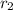 равна разности потенциальных энергий этих конфигураций, удельных к длине:
равна разности потенциальных энергий этих конфигураций, удельных к длине:
Работа, удельная к длине, совершаемая полем при увеличении расстояния между струнами от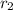 до
до 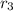 будет равна:
будет равна: 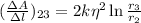 ;
;
Учитывая, что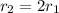 ,
,
и, кроме того, поскольку: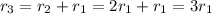 , то:
, то:
Стало быть:
Отсюда: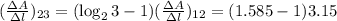 мДж/м
мДж/м 
= 1.843 мДж/м .