Катер перетинки річку. ширина якої 120 м, тримаючи курс перпендикулярно до тече. Визначити відстань, на яку несе течія катер пд час переправи, якщо швидкість катера відносно води 2.4 м/с, а швидкість течії 0.7 м/с? Яка швидкість катера відносно берегів

Вверху горки телообладало потенциальной энергией  mgh

НО поскольку ты не знаешь высоту горки, а знаешь только ее длину, то выразим это.

Длина горки это гипотенуза, а высота катет лежащий напротив угла в 30 градусов. sin30= 0,5 = отношению противолежащего катета к гипотенузе. Отсюда находим, что высота горки равна 6 м.

Внизу горки, у ее основания, тело обладало только кинетической энергией (mV^2)/2

Поскольку в конце пути тело остановилось, то, значит, кинетическая энергия стала равна нулю, и получается, что вся энергия ушла на работу силы трения F*S  F=Mmg А=MmgS (М - коэффициент трения).

подставляем закон сохранения энергии 

mgh=(mV^2)/2=MmgS

кинетическая энергия нам здесь вообще не понадобится, поэтому запиши это равенство без (mV^2)/2

mgh=MmgS  Массы сокращаются, g тоже сокращается и получаем, что S=h/M = 6/0,05=120м

Будем считать, что сила трения качения пренебрежимо мала, а также пренебрежем сопротивлением воздуха. Тогда для обоих случаев должен выполняться закон сохранения полной механической энергии.

 1) Таким образом в обоих случаях цилиндры движутся под действием составляющей силы тяжести параллельной наклонной плоскости. Из второго закона Ньютона получим:

          , отсюда 

           --------(1)

где - ускорение поступательного движения цилиндра.

       С другой стороны ускорение равно:

           -------(2)

где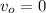 - начальная скорость (по условию)

       - скорость цилиндра через промежуток времени , когда он коснется первый раз горизонтали.  

Из (1) и (2) найдем искомое время :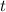

             ---------(3)

2) Конечную скорость найдем с закона сохранения механической энергии:

------(4)

      ------(5)

где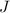 - момент инерции цилиндра относительно его оси симметрии;

  --------(6)

       - угловая скорость вращения цилиндра 

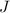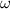Подставим в (4) вместо  и  выражения (5) и (6), получим после сокращения: 

 , отсюда

          ----------(7)

Подставим в (3) вместо выражение (7), получим расчетную формулу для искомого времени:           

Расчет времени:

а) Для сплошного цилиндра, для которого :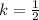

        с

б) Для тонкостенного цилиндра, для которого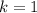 :