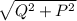Катушка массой m подвешена за намотанную на нее нить к
вертикальной стене, как показано на рис. 13.25. Малый радиус катушки r , большой R , коэффициент трения между катушкой и стеной μ.
При каком наименьшем угле α между нитью и стеной катушка не будет скользить по стене?
F=G*m₁*m₂/R²
гравитационная постоянная - G=6.67*10⁻¹¹ Н*м/kg²
g=G*Mз/(Rз+h)² - ускорение свободного падения, где Мз - масса Земли, а Rз - радиус Земли
На поверхности Земли h=0
g=G*Mз/Rз²
равномерное движение по окружности является равноускоренным,т.к. есть нормальное (центростремительное) ускорение ,равное v²/R и постоянное во времени.
а=v²/R
первая космическая скорость - скорость, которую нужно сообщить телу, чтоб оно стало искусственным спутником Земли (двигалось по круговой орбите вокруг Земли)
v= √GMз/Rз Этот главный для астрономии закон выведен И.Ньютоном в 1687 г. опытным путем (и, насколько мне известно, до сих пор не подтвержден теоретически). Закон утверждает, что два точечных тела с массами m1 и m2 притягивают друг друга с силой
В трехфазных цепях, так же как и в однофазных, пользуются понятиями активной, реактивной и полной мощностей.
В общем случае несимметричной нагрузки активная мощность трехфазного приемника равна сумме активных мощностей отдельных фаз
P = Pa + Pb + Pc
(Pa = Ua Ia cos φa; Pb = Ub Ib cos φb; Pc = Uc Ic cos φc)
Ua, Ub, Uc; Ia, Ib, Ic – фазные напряжения и токиφa, φb, φc – углы сдвига фаз между напряжением и током.
Реактивная мощность соответственно равна алгебраической сумме реактивных мощностей отдельных фаз:
Q = Qa + Qb + Qc
Qa = Ua Ia sin φa; Qb = Ub Ib sin φb; Qc = Uc Ic sin φc.
Полная мощность отдельных фаз
Sa = Ua Ia; Sb = Ub Ib; Sc = Uc Ic.
Полная мощность трехфазного приемника
S =