Корпуси мобільних телефонів виготовляють з полімерного матеріалу. Визначте густину, якщо зразок такого полімеру при об'ємі 6 см3 має масу 7,2 г. Відповідь: 1200 кг/м3

• изначально давление газа определялось суммой давлений атмосферы P0  и поршня P1 (они компенсируют друг друга, и потому поршень покоится)

○ давление поршня определяется выражением P1 = F1/S = (Mg)/S, где M - масса поршня

• затем, когда температуру газа повысили вдвое, давление поршня изменилось, так как на него положили груз массой m: P2 = F2/S = ((m + M)g)/S

• напишем уравнения состояния газов

○ (P0 + (Mg)/S) V = v R T
○ (P0 + ((m + M)g)/S) V = 2 v R T

• разделив уравнения друг на друга, находим массу груза

◘ m = (P0 S)/g + M = 15 кг

По закону всемирного тяготения сила взаимодействия

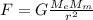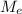1) , где — масса Земли, 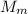— масса Луны, — радиус орбиты Луны.

С другой стороны, Луна движется только с центростремительным ускорением, значит по II закону Ньютона

2)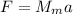 , где — центростремительное ускорение;

3)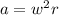 , где 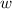— угловая скорость;

4)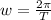 , где 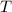— период обращения Луны вокруг Земли;

5)

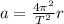
6)

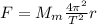
Тогда

7)

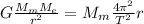
8)

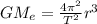
К слову, масса Земли, которая фигурирует в последней формуле, была вычислена в 1798 году Генри Кавендишем на основе уже известного в то время радиуса Земли. Радиус же Земли был вычислен опытным путём в 240 году до нашей эры Эратосфеном Киренским. Поэтому предлагаю перейти в нашей формуле от массы Земли к радиусу Земли. Мы знаем, что тело на поверхности Земли движется с ускорением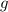 , и на основе вышеизложенного можем написать аналогичное уравнение

9)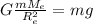 , где 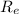— радиус Земли;

10)

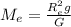
Подставим массу Земли в формулу 8.