Квадрат ABCD , вырезанный из тонкого ровного листа жести, скользит по плоской поверхности. В некоторый момент времени скорость вершины A равна v = 1 м/с и направлена к вершине B , а угловая скорость вращения квадрата ω = 4 рад/с. Длина стороны квадрата a = 25 см. Чему равны величины скоростей остальных вершин квадрата (перечислить в порядке возрастания)? ответы выразите в м/с, округлив до сотых. Направление обхода вершин квадрата совпадает с направлением его вращения.
ответ: 1.4м/c 1м/c 1м/c 0м/c
Объяснение:
Мгновенный центр вращения квадрата располагается на перпендикуляре к скорости v, а значит лежит на прямой AD. Известно, что угловая скорость вращения ω =4 рад/c. Чтобы найти скорость v, нужно умножить расстояние от центра вращения на угловую скорость вращения. Определим расстояние от центра вращения:
x =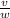 = 0.25м
= 0.25м
Заметим, что это расстояние в точности равно стороне квадрата. Известно, что скорость v направлена к точке В, а также, что направление обхода вершин квадрата совпадает с направлением его вращения. Это значит, что из двух точек лежащих на прямой AD, нам подходит только точка D => точка D является мгновенным центром вращения и ее скорость равна 0.
Теперь легко определяем скорости точек C и B:
Vc = ωa = 1м/c
Vb = ω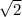 a = 1.4 м/c
a = 1.4 м/c