ЛАБОРАТОРНА РОБОТА № 9
Тема. Визначення коефіцієнта тертя Ковзання.

Показать ответ

Ответ:

badery346

29.04.2021 19:38

Плотность чугуна 11,34 г/см³, поэтому шар массой 2,8 кг имеет полезный объем

2800 / 11,34 ≈ 247 см³. Следовательно, объем полости шара 500 - 247 = 253 см³

2)Дано V кирасина=0,8 дм^3

плотность стали=7800 кг/м^(3) = p

найти массу детали.

m=p*V

переведем значение объема в единицы Си

0,8 дм^3=8*10^(-4) м^3

7800*8*10^(-4)=6,24 кг

3)первую четверть пути - S автомобиль двигался со скоростью 60 км/ч

потратил время t1=S/60

остальной путь- 3S со скоростью 20 км/ч. потратил время t2 =3S/20

общее расстояние -4S со скоростью Vср потратил время t1+t2 =4S/Vср

составим уравнение

4S/Vср =S/60 +3S/20

4/Vср =1/60 +3/20

Vср=24 км/ч

На

0,0(0 оценок)

Ответ:

yul19758694

23.04.2020 17:17

0,16 Ом

Объяснение:

Разобьем проводник на элементарные элементы длинной dx и площадью S(x) очевидно, сопротивление одного того элемента равно:

$\displaystyle dR=\rho\frac{dx}{S(x)}$

Установим вид функции S(x). Зависимость радиуса проводника от его длины представляет линейную функцию вида y=kx+b, найдем ее коэффициенты решив следующую СЛУ:

$\displaystyle k*0+b=10^{-3}$

$\displaystyle k*1+b=2*10^{-3}$

Откуда b=10⁻³, k=10⁻³

Таким образом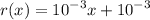 $\displaystyle r(x)=10^{-3}x+10^{-3}$

Площадь поперечного сечения проводника:

$\displaystyle S(x)=\pi r^2(x)=\pi (10^{-3}x+10^{-3})^2=10^{-6}\pi (x+1)^2$

Сопротивление всего проводника найдем как предельную сумму сопротивлений его элементарных длин (они соединены последовательно):

$\displaystyle R=\int\limits^1_0 {} \, dR =\frac{\rho}{10^{-6}\pi } \int\limits^1_0 {\frac{dx}{(x+1)^2} }$

Берем интеграл:

$\displaystyle R=-\frac{\rho}{10^{-6}\pi }* \frac{1}{x+1} |_0^1=-\frac{\rho}{10^{-6}\pi } *\frac{1}{2}+\frac{\rho}{10^{-6}\pi } =\frac{\rho}{2*10^{-6}\pi }$