Так как скорость мальчика составляет долю 0,6 от скорости течения реки, то перемещение мальчика не может быть направлено перпендикулярно течению реки. В этом можно убедится, сделав следующие построения. Обозначим скорость течения u (на рисунке направлена горизонтально, 5 клеточек), скорость мальчика относительно реки обозначи v₀ (v₀=nu, по условию задачи n=0,6; однако стоит отметить, что в конце задачи получим формулу для решения любого n, при условии, что 0<n≤1) (v₀ возьмем за 3 клеточки). Чтобы найти вектор направления скорости мальчика относительно берега V, нам надо знать точку конца этого вектора. Для этого из конца вектора u проведем окружность радиуса v₀. Обращаем внимание, что если провести касательную АВ (см. рис.), то, т.к. вектор перемещения сонаправлен с вектором скорости V, то расстояние, на которое снесет мальчика ΔX=BC окажется наименьшим при данной скорости относительно реки v₀ (это и есть оптимальная стратегия!). Итак, мы получили прямоугольный треугольник АВС, в котором ΔX=BC (смещение, которое нужно найти), L=AC (ширина реки, по условию 120 м) и AB (перемещение мальчика относительно берега),
1. Введем прямоугольную систему координат. Ось Оу направлена перпендикулярно течению, Ох - вдоль реки.
2. Мальчик участвует в двух движениях одновременно: он перемещается вдоль берега (Ох) со скоростью V*cosα = u - v₀*cosα, и он плывет перпендикулярно течению (Оу) со скоростью v₀*sinα.
Пусть время t - время за которое мальчик переплывет реку. Так как он плывет равномерно прямолинейно, то согласно законам кинематики:
ΔX=(u-v₀*cosα)t (1)
L=v₀*sinα*t (2)
3. Так как направление скорости V совпадает с касательной, то по св-ву касательной вектор V перпендикулярен вектору v₀. Таким образом u*cosα=v₀.
С другой стороны v₀=nu, значит cosα=n, согласно осн. тригонометрическому тождеству: sinα=√1-
4. Из равенств 1 и 2 следует, что:
((u-v₀*cosα)*L) / (v₀*sinα)=ΔX
И в итоге:
ΔX = (L/n) * √
В нашем случае:
ΔX = 160 м
Напоминаю, что полученная формула справедлива для любого 0<n≤1
1. Изначально, до того как самосвал проехал по заснеженной дороге (будем рассматривать участок длиной L), линейную плотность снега на этой дороге λо (лямбда нулевое) можно вычислить следующим образом: λо=M/L, где М - масса снега на заснеженной дороге, L - ее длина.
2. После того, как самосвал проехал участок длиной L со скоростью u = 20м/с за время T₁ (L=u*T₁), из отверстия в его кузове высыпался снег массой ΔM₁. По условию снег сыпется равномерно со скоростью k =3кг/c. Таким образом, ΔM₁=k*T₁.
Теперь на заснеженной дороге равномерно на каждый метр распределился снег массой M+ΔM₁, то есть линейная плотность (всего!) снега равна: λ₁=(M+ΔM₁)/L (3).
3. Теперь самосвал выехал за пределы рассматриваемого участка длиной L, по условию вдогонку выехал комбайн с пустым бункером, который вмещает в себя массу m снега. Рассмотрим движение комбайна на участке L.
а) Так как на каждом метре дороги равномерно распределено одинаковое количества снега с плотностью λ₁, то, считая, что комбайн до момента заполнения бункера путь x₁, можно вычислить массу снега в бункере следующим б) Так как комбайн двигался равномерно со скоростью V, то, считая, что бункер заполнился за время t₁, получается: x₁=V*t₁.
Таким образом из пп. а-б получается, что: m=λ₁*V*t₁ (1).
4. Теперь рассмотрим вторую часть задачи. По условию: "если бы скорость самосвала была в 3 раза большей, то время заполнения бункера увеличилось бы в 2 раза, при неизменной скорости комбайна" (t₂=2t₁, u₂=3u) Значит, рассуждая аналогично пункту 1:
(качественный анализ)
Так как скорость мальчика составляет долю 0,6 от скорости течения реки, то перемещение мальчика не может быть направлено перпендикулярно течению реки. В этом можно убедится, сделав следующие построения. Обозначим скорость течения u (на рисунке направлена горизонтально, 5 клеточек), скорость мальчика относительно реки обозначи v₀ (v₀=nu, по условию задачи n=0,6; однако стоит отметить, что в конце задачи получим формулу для решения любого n, при условии, что 0<n≤1) (v₀ возьмем за 3 клеточки). Чтобы найти вектор направления скорости мальчика относительно берега V, нам надо знать точку конца этого вектора. Для этого из конца вектора u проведем окружность радиуса v₀. Обращаем внимание, что если провести касательную АВ (см. рис.), то, т.к. вектор перемещения сонаправлен с вектором скорости V, то расстояние, на которое снесет мальчика ΔX=BC окажется наименьшим при данной скорости относительно реки v₀ (это и есть оптимальная стратегия!). Итак, мы получили прямоугольный треугольник АВС, в котором ΔX=BC (смещение, которое нужно найти), L=AC (ширина реки, по условию 120 м) и AB (перемещение мальчика относительно берега),
1. Введем прямоугольную систему координат. Ось Оу направлена перпендикулярно течению, Ох - вдоль реки.
2. Мальчик участвует в двух движениях одновременно: он перемещается вдоль берега (Ох) со скоростью V*cosα = u - v₀*cosα, и он плывет перпендикулярно течению (Оу) со скоростью v₀*sinα.
Пусть время t - время за которое мальчик переплывет реку. Так как он плывет равномерно прямолинейно, то согласно законам кинематики:
ΔX=(u-v₀*cosα)t (1)
L=v₀*sinα*t (2)
3. Так как направление скорости V совпадает с касательной, то по св-ву касательной вектор V перпендикулярен вектору v₀. Таким образом u*cosα=v₀.
С другой стороны v₀=nu, значит cosα=n, согласно осн. тригонометрическому тождеству: sinα=√1-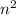
4. Из равенств 1 и 2 следует, что:
((u-v₀*cosα)*L) / (v₀*sinα)=ΔX
И в итоге:
ΔX = (L/n) * √
В нашем случае:
ΔX = 160 м
Напоминаю, что полученная формула справедлива для любого 0<n≤1
ответ: 160 м
Итак, поехали.
1. Изначально, до того как самосвал проехал по заснеженной дороге (будем рассматривать участок длиной L), линейную плотность снега на этой дороге λо (лямбда нулевое) можно вычислить следующим образом: λо=M/L, где М - масса снега на заснеженной дороге, L - ее длина.
2. После того, как самосвал проехал участок длиной L со скоростью u = 20м/с за время T₁ (L=u*T₁), из отверстия в его кузове высыпался снег массой ΔM₁. По условию снег сыпется равномерно со скоростью k =3кг/c. Таким образом, ΔM₁=k*T₁.
Теперь на заснеженной дороге равномерно на каждый метр распределился снег массой M+ΔM₁, то есть линейная плотность (всего!) снега равна: λ₁=(M+ΔM₁)/L (3).
3. Теперь самосвал выехал за пределы рассматриваемого участка длиной L, по условию вдогонку выехал комбайн с пустым бункером, который вмещает в себя массу m снега. Рассмотрим движение комбайна на участке L.
а) Так как на каждом метре дороги равномерно распределено одинаковое количества снега с плотностью λ₁, то, считая, что комбайн до момента заполнения бункера путь x₁, можно вычислить массу снега в бункере следующим б) Так как комбайн двигался равномерно со скоростью V, то, считая, что бункер заполнился за время t₁, получается: x₁=V*t₁.
Таким образом из пп. а-б получается, что: m=λ₁*V*t₁ (1).
4. Теперь рассмотрим вторую часть задачи. По условию: "если бы скорость самосвала была в 3 раза большей, то время заполнения бункера увеличилось бы в 2 раза, при неизменной скорости комбайна" (t₂=2t₁, u₂=3u) Значит, рассуждая аналогично пункту 1:
λ₁=(M+ΔM₂)/L (4);
ΔM₂=k*T₂.
аналогично пункту 2:
L=3u*T₂
аналогично пункту 3:
m=λ₂*V*t₂=λ₂*V*2t₁ (2)
Приравнивая равенства 1 и 2, получаем:
2*λ₂=λ₁
Учитывая равенства 3 и 4, получаем:
(M+k*T1)/L=2*(M+k*T2)/L
Далее, путем нехитрых преобразований:
λо+k/u=2λо+2k/3u
И в конечном итоге:
λо=k/(3u)
λо=50 г/м
ответ: 50 г/м