Лыжник стартует с нулевой скоростью с высоты H холма, склон которого составляет постоянный угол α. Съехав с этого холма и проехав по горизонтальному участку расстояние L, он заезжает до другой холм высоты h (h µ0), то какая должна быть наименьшая начальная скорости лыжника на вершине первого холма, чтобы он смог заехать на вершину второго? Решить задачу
1) Применяя только законы Ньютона и формулы из кинематики,
2) Применяя закон об изменении механической энергии,
и сравнить ответы.
а) для x1 - x0=0 | Для x2 - x0=90
б) проекцию начертишь (см объяснение)
в) В 60м через 1 секунду
Объяснение:
x - координата в момент времени t
x0 - начальная координата
Vx - проекция скорости на ось
Рисуешь линию, отмечаешь 0 и 90, рисуешь стрелки чтобы смотрели друг на друга, где 0 пишешь над стрелкой V1, где 90 соотв. V2, это будет проекция вроде как.
V [м/с]. S=90м (расстояние), V=|V1| + |V2|=90м/с, значит, они встретятся через секунду, записать это можно так: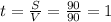
Где встречаются? Если у одного скорость 60м/с, у другого -30м/с, а начальная у первого 0, у второго 90, а время 1с, то 0+60 и 90-30 => 60м
Как-то так. Я в физике на 3-4 учусь, по логике мне проще объяснить, чем по формулам :)
X – больший заряд
У – меньший
(x+y)/2 - заряд после соприкосновения
х - (x+y)/2 = (х-у)/2 – уменьшение большего заряда
(х-у)/2 : x = 40 : 100
(х-у): x = 80 : 100
1- у/x = 0,8
у/x = 1 – 0,8 = 0,2 = 1:5
y:x = 1:5
Два одинаковых металлических шарика с одноименными зарядами привели в соприкосновение. При этом заряд одного из них УВЕЛИЧИЛСЯ на 40%. Найдите отношение начальных зарядов шариков.
X – больший заряд
У – меньший
(x+y)/2 - заряд после соприкосновения
(x+y)/2 - у = (х-у)/2 – увеличение меньшего заряда
(х-у)/2 : у = 40 : 100
(х-у): у = 80 : 100
х/y- 1 = 0,8
x/y = 1 + 0,8 = 1,8
x:y = 1,8:1 = 9:5