Маленький шарик массой m, надетый на горизонтальную гладкую спицу между двух пружин жёсткостью k, совершает гармоничные колебания с амплитудой а. концы пружин прикреплены к вертикальным стенкам. определите, как измеряется период колебаний шарика и максимальная кинетическая энергия шарика, если систему заменить на другую, изображённую на рисунке 2 при неизменной амплитуде колебания.
для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
запишите выбранные 2 цифры для каждой величины. цифры в ответе могу повторяться.
Δt≈10,95(градус цельсия)
Объяснение:
ДАНО: СИ:
m=20кг
m бензина=20г 0.02кг
с воды =4200 Дж/ кг * С(градус цельсия)
q бензина = 46 000 000Дж/кг
НАЙТИ:
Δt -?
Q(сгорания бензина) = Q(нагревание воды)
Q(сгорания бензина)= q*m = 46*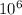
Дж/ кг * 0.02кг = 920 000 Дж
Q(нагревание воды)=c*m*Δt
Δt = Q/(c*m)= 920000 Дж / 4200 Дж/ кг * С * 20кг =10,952380952 C(градус цельсия)
1. Первым свойством электромагнитной волны является то, что она поперечна.
2. Скорость распространения электромагнитной волны зависит от характеристик среды.
3. Во время распространения электромагнитной волны в пространстве в ней происходит преобразование электрического поля в магнитное и наоборот.
4. Электромагнитная волна обладает механическим импульсом.
5. Возбуждение волн может вызываться только зарядами, которые движутся с ускорением.
Основные причины потери энергии в трансформаторах:
1. Активные сопротивления обмоток.
2.Токи Фуко в сердечнике