Численное значение ускорения свободного падения не играет никакой роли. И на Луне и на Марсе время достижения максимальной скорости было бы одинаковым. Отличалась бы только сама эта максимальная скорость. Поскольку, как хорошо известно, частота пружинных колебаний в продольном однородном потенциальном поле происходят с той же частотой, что и в его отсутствии. Каждую четверть периода гармонических колебаний – модуль скорости меняет своё значение от нулевого до амплитудного и наоборот.
БЕЗ ДОКАЗАТЕЛЬСТВА ФАКТА НЕИЗМЕННОМТИ ПЕРИОДА КОЛЕБАНИЙ:
сек ;
ВТОРОЙ с доказательством неизменности периода:
Будем для начала откладывать координату вниз от начального положения груза. На груз всё время будет действовать сила:
Теперь станем откладывать координату от точки и получим смещённую координату:
и теперь уже можем записать уравнение для силы так:
Последнее – это уравнение гармонических колебаний с циклической частотой:
и периодом:
нас интересует четверть-период, так что:
сек ;
ТРЕТИЙ с доказательством неизменности периода:
На груз всё время будет действовать сила:
Это уравнение гармонических колебаний с циклической частотой:
и периодом:
нас интересует четверть-период, так что:
сек ;
ЧЕТВЁРТЫЙ с доказательством неизменности периода:
Будем откладывать координату вниз от начального положения груза. По закону сохранения энергии:
Возьмём производную от обеих частей уравнения:
Это уравнение гармонических колебаний с циклической частотой:
1. Сила тока это по сути поток электрического заряда через поперечное сечение проводника. То есть сила тока в 1 А означает, что за 1 с через поперечное сечение проводника пройдёт заряд в 1 Кл. В данной задаче сила тока I=0.1 А, значит за 1 с проходит 0,1 Кл. Так как нужно 10 Кл, то для нахождения времени надо разделить t=10/0,1=100 c. 2. Удельное электрическое сопротивление проводника равно r=R*S/l, где R - электрическое сопротивление всего проводника, S - площадь поперечного сечения проводника, l - длина проводника. Для меди r=0.0175 мкОм*м. Отсюда находим площадь поперечного сечения проводника: S=rl/R; Плотность меди равна p=892 кг/м^3. Получаем массу проводника: m=pV; m=plS; m=prl^2/R; m=892*1.75*10^-8*10^6/2; m=7.805 кг.
Численное значение ускорения свободного падения не играет никакой роли. И на Луне и на Марсе время достижения максимальной скорости было бы одинаковым. Отличалась бы только сама эта максимальная скорость. Поскольку, как хорошо известно, частота пружинных колебаний в продольном однородном потенциальном поле происходят с той же частотой, что и в его отсутствии. Каждую четверть периода гармонических колебаний – модуль скорости меняет своё значение от нулевого до амплитудного и наоборот.
БЕЗ ДОКАЗАТЕЛЬСТВА ФАКТА НЕИЗМЕННОМТИ ПЕРИОДА КОЛЕБАНИЙ:
ВТОРОЙ с доказательством неизменности периода:
Будем для начала откладывать координату вниз от начального положения груза. На груз всё время будет действовать сила:
Теперь станем откладывать координату от точки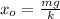 и получим смещённую координату:
и получим смещённую координату:
Последнее – это уравнение гармонических колебаний с циклической частотой:
ТРЕТИЙ с доказательством неизменности периода:
На груз всё время будет действовать сила:
Это уравнение гармонических колебаний с циклической частотой:
ЧЕТВЁРТЫЙ с доказательством неизменности периода:
Будем откладывать координату вниз от начального положения груза. По закону сохранения энергии:
Возьмём производную от обеих частей уравнения:
Это уравнение гармонических колебаний с циклической частотой:
В данной задаче сила тока I=0.1 А, значит за 1 с проходит 0,1 Кл. Так как нужно 10 Кл, то для нахождения времени надо разделить t=10/0,1=100 c.
2. Удельное электрическое сопротивление проводника равно r=R*S/l, где R - электрическое сопротивление всего проводника, S - площадь поперечного сечения проводника, l - длина проводника. Для меди r=0.0175 мкОм*м. Отсюда находим площадь поперечного сечения проводника: S=rl/R;
Плотность меди равна p=892 кг/м^3.
Получаем массу проводника: m=pV;
m=plS;
m=prl^2/R;
m=892*1.75*10^-8*10^6/2;
m=7.805 кг.