Можно ли сделать так чтобы внутренние энергии тела над которым совершают работу осталось незаменимой если можно то как это сделать

Показать ответ

Ответ:

marigol0220

16.10.2021 00:52

$\rho=1,29$ кг/м3 - плотность воздуха

g=9,8 м/с2

V=1600 м3

m=450 кг

Найти предельное значение массы груза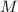

Будем считать, что шар с грузом поднимается достаточно медленно для того, чтобы силой сопротивления воздуха можно было пренебречь. Тогда на шар действует две силы - сила тяжести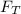 $F_{T}$ и подъемная сила $F_{A}$ .

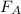Чтобы шар начал подниматься должно выполняться условие:

$F_{A}F_{T}$ -------(1)

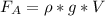При этом $F_{A}=\rho*g*V$ --------(2)

$F_{T}=(m+M)*g$ -------(3)

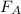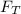Подставим в (1) вместо $F_{A}$ и $F_{T}$ выражения (2) и (3):

$\rho*g*V(m+M)*g$ , отсюда

$M<(\rho*V-m)=1,29*1600-450=1614$ кг

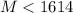ответ: M<1614 кг

0,0(0 оценок)

Ответ:

аникдим

25.12.2021 09:47

Дано: масса цинка (m) - 4 кг, начальная температура цинка (t₁) - 20°C, конечная температура цинка (t₂) - 420°С, удельная теплоемкость цинка (с) - 380 Дж/кг*°С, удельная теплота плавления (λ) - 12*10⁴ Дж/кг

Найти: количество энергии, требуемой для нагревания и расплавления цинка (Q).

Найдем количество энергии, требуемой для нагревания цинка - Q₁=cm(t₂-t₁)=380*4*400=608*10³ Дж

Найдем количество энергии, требуемой для расплавления цинка - Q₂=λm=12*10⁴*4=480*10³ Дж

Найдем количество энергии, требуемой для нагревания и расплавления цинка - Q=Q₁+Q₂=608*10³+480*10³=10³(608+480)=1088*10³ Дж=1088 кДж

ответ: 1088 кДж

Объяснение:

надеюсь

0,0(0 оценок)

Популярные вопросы: Физика