При нормальном падении света на дифракционную решетку, синус угла под которым будет виден некоторый интерференционный максимум дифракционной решетки можно найти по формуле sin(a) = m *L/S; где (а) – угол, под которым виден какой-либо максимум решетки; m – порядковый номер максимума, m = 3; L – длина волны света, L = 500 нм; S – период дифракционной решетки, S = 6 мкм. При вычислении период решетки и длину волны следует применять в одной и той же размерности. Выразим и то и другое в мкм. Тогда sin(a) = 3 * 0,5/6 = 0,25. Угол (а) под которым будет виден максимум 3-го порядка (а) = arcsin0,25 = 14,4775… градусов.
Частота - это число колебаний в единицу времени , где n - число колебаний, t - промежуток времени (с). Вычислим: Герц.
Период обратен частоте т.е. . Вычислим:
По формуле математического маятника , где l - длина маятника (м), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²). В системе СИ: 40 см = 0,4 метра. Подставляем числовые значения и вычисляем:
По формуле математического маятника , где l - длина маятника (м), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²). Подставляем и вычисляем: период:
Частота следовательно будет равна: Гц
Используем две формулы периода , где l - длина маятника (м), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²) и
Левые части формул равны, следователь и правые части также равны:
Частота - это число колебаний в единицу времени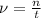 , где n - число колебаний, t - промежуток времени (с). Вычислим:
, где n - число колебаний, t - промежуток времени (с). Вычислим: 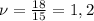 Герц.
Герц.
Период обратен частоте т.е.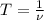 . Вычислим:
. Вычислим: 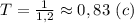
По формуле математического маятника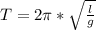 , где l - длина маятника (м), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²). В системе СИ: 40 см = 0,4 метра. Подставляем числовые значения и вычисляем:
, где l - длина маятника (м), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²). В системе СИ: 40 см = 0,4 метра. Подставляем числовые значения и вычисляем: 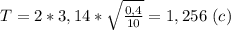
По формуле математического маятника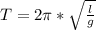 , где l - длина маятника (м), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²). Подставляем и вычисляем: период:
, где l - длина маятника (м), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²). Подставляем и вычисляем: период: 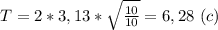
Частота следовательно будет равна: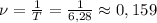 Гц
Гц
Используем две формулы периода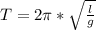 , где l - длина маятника (м), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²) и
, где l - длина маятника (м), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²) и 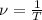
Левые части формул равны, следователь и правые части также равны:
Распишем частоту: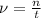
Подставляем и вычисляем: