На земле лежит прямоугольная чугунная плита, площадь основания которой равна 1,2 м в квадрате, а толщина — 18 см. какова масса плиты? определи давление плиты на землю. принять g=9,8 н/кг. используй таблицу плотности веществ. ответ (при необходимости ответ округли до тысячных): m=p=

Показать ответ

Ответ:

Kusya2003

03.03.2022 03:15

Прямолинейное равноускоренное движение (можно назвать его равнозамедленным, так как ускорение отрицательно)

3 м/с

1 с

6 м

Объяснение:

Движение тела описывается уравнением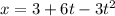 $x = 3+6t-3t^{2}$ .

Уравнением вида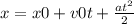 $x=x0+v0t + \frac{at^{2} }{2}$ (где х0 — начальная координата, v0 — начальная скорость, а — ускорение, t — время) описывается прямолинейное равноускоренное движение.

Уравнение движения, данное в условии, является уравнением того же вида, значит, движение тела — прямолинейное равноускоренное.

Проведя аналогию между двумя уравнениями, заметим что в уравнении

$x=3+6t-3t^{2}$

х0 = 3

v0 = 6

$\frac{a}{2}$ = -3 ⇒ a = -3*2 ⇒ a=-6.

Скорость тела при прямолинейном равноускоренном движении находится по формуле

v = v0 + at.

Подставим в эту формулу значения (v0 = 6 м/с; а = -6 м/с2; t = 0,5 с):

v = 6 м/с + (-6) м/с2 * 0,5 с = 6 м/с - 3 м/с = 3 м/с

Тело остановится, когда его скорость будет равна нулю. Воспользуемся той же формулой скорости при равноускоренном движении, что и в предыдущем пункте:

v = v0 + at

0 = 6 -6t

6t = 6

t = 1 (с)

В предыдущем пункте уже было посчитано, что тело остановится через t=1 c. Подставим это время в уравнение движения (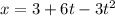 $x=3+6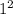t -3t^{2}$ ):

x = 3 + 6*1 - 3* $1^{2}$ = 6 (м).

0,0(0 оценок)

Ответ:

Хорошист992017

25.03.2021 22:03

Пусть общий путь S, общее время движения t, тогда средняя скорость:
Vср = S / t.

Рассмотрим первую половину пути:
S₁ = (S/2)
t₁ = S₁/V₁ = S / (2*V₁) = S / 20 = (1/20)*S = 0,05*S ч

Рассмотрим вторую половину пути.
Оставшийся путь
S₂ = (S/2)
Оставшееся время t₂ разобьем на 3 равных промежутка по (t₂ /3) часа

Путь на первой трети остатка:
S₂₁ = V₂₁*(t₂/3) = (20/3)*t₂

Путь на второй трети остатка:
S₂₂ = 0 (ремонт!)

Путь на последней трети остатка:
S₂₃ = V₂₃*(t₂/3) = (5/3)*t₂

Собираем
S₂ = S₂₁+S₂₂+S₂₃ = (20/3)*t₂ + 0 + (5/3)*t₂ = (25/3)*t₂
(S/2) = (25/3)*t₂
t₂ = (3/50)*S = 0,06*S ч

Общее время:
t = t₁ +t₂ = 0,05*S + 0,06*S = 0,11*S

Средняя скорость:
Vcp = S / (0,11*S) = 1 / 0,11 ≈ 9 км/ч

0,0(0 оценок)

Популярные вопросы: Физика